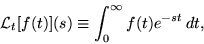=======================================================================
Cybernetics in the 3rd Millennium (C3M) -- Volume 2 Number 9, Sep. 2003
Alan B. Scrivener --- www.well.com/~abs --- mailto:abs@well.com
=======================================================================
Do Nothing, Oscillate, or Blow Up:
An Exploration of the Laplace Transform
The last two issues of C3M ranged pretty far afield from what most
people think of as cybernetics. I got an unusually high number of
positive comments back, but I also got my first unsubscribe request.
So this month I am returning to the mainstream, and plunging into
some heavy-duty mathematics as well. Here goes...
I am sometimes amazed to encounter people who say they are very
interested in cybernetics and/or systems theory but they don't like
math. It seems to me that without math these pursuits quickly devolve
into just word games, or at best the kind of paying attention to
externalities and relationships that brought us group therapy in
psychology and man-in-the-loop testing in engineering. Math is
vital to the study of systems because it helps us understand all of
the things systems are CAPABLE of doing, that is, all possible
behavioral modes of a given set of assumptions.
In the 1930s Lewis Fry Richardson was a pioneer of the application
of mathematical models to social science. His "Generalized Foreign
Policy" (1939) offered a mathematical model of arms races, and
generated a firestorm of criticism from the "experts" in foreign
policy and diplomacy. His next book was "Arms and insecurity: a
Mathematical Study of the Causes and Origins of War" (1949).
( www.amazon.com/exec/obidos/ASIN/0835703789/hip-20 )
In it he devoted quite a few pages to rebutting his critics.
They had claimed that you couldn't reduce the complexities of
international relations to mathematical equations, because it
required human judgment and intuition to analyze these types of
problems. Richardson's main argument was that when people propose
a hypothesis in this (or any) field they often state the "obvious"
conclusions from that hypothesis incorrectly; their conclusions
do not follow "logically" from their premises. Only the rigor
of math can verify such conclusions.
Likewise, more recently, misguided critics have attacked the
methodology of computer modeling as if working things out
"in your head" represented a superior and more reliable way
to test if conclusions follow from premises.
For example, in his essay "Understanding the counterintuitive
behavior of social systems" (1971) Jay W. Forrester described
how government funded low income housing projects would usually
aggravate the lack of affordable housing, by attracting more
people to an area than the projects provide. His models showed
that somehow creating more jobs instead would cause private investors
to overbuild new housing, increasing supply and reducing cost.
The essay is reprinted in "Collected Papers of J. W. Forrester" (1975).
( www.amazon.com/exec/obidos/ASIN/1563271923/hip-20 )
So, if math is so vital to cybernetics and systems theory, why
do many of the fans of these fields hate and avoid math? I think
it is because it is so badly taught to our children. Kids are
very aware of rules, and have high standards of integrity.
Our standard math curriculum lies to them, and this turns a
lot of them off. We could tell them, "We're going to make
up some rules this year and follow them and next year we're
going to change the rules." But no, we say, "You can't subtract
a larger number from a smaller one," and then the next year
we say, "Surprise! You can after all, and the answer is a new
kind of number, called a negative number." That scrapes a few
of them off. Then we pull the same trick with division, and
surprise them with fractions. Then we do it again with square
roots, telling them you "can't" take the square root of a negative
number, only to go back on our word and introduce "i" the "imaginary"
quantity. By this time we've lost almost all of them. Even
the people who TEACH math to grade schoolers are pretty nervous
about i in my experience. And yet "complex" numbers (formed
adding "real" and "imaginary" numbers) are among the most powerful
and elegant tools in mathematics. (This goes along with my theory
that the purpose of public education is to inoculate people against
knowledge so they don't catch it later in life.)
I was fortunate in that I had some very good teachers, including
my father who taught me at home, and the inoculation never "took"
with me. I hung in there through the lies and "got it" time and
time again. By 9th grade I had noticed a pattern: We were taught
to count. Then counting was generalized to addition (which was
"closed" over the counting numbers, or positive integers, i.e., add
any two counting numbers and you get another counting number).
Then we learned the inverse of addition, subtraction: which was
not "closed" over the counting numbers. They had to introduce
negative numbers to make a complete set of numbers.
Then addition was generalized to multiplication (which was
"closed" over the integers), and we learned the inverse of
multiplication: division, which was not "closed" over the
integers. They had to introduce fractions to make a complete
set of numbers (and we still couldn't divide by zero).
Then multiplication was generalized to powers (which was
"closed" over the rational numbers -- as long as the exponents
were whole), and we learned the inverse of powers: roots, which
were not "closed" over the rationals. They had to introduce
irrationals to make a complete set of numbers (and we still
couldn't take the square root of minus one).
At this point I came up with what I call Scrivener's Conjecture:
Every time we generalize an operator and then take its
inverse we will have to invent a new kind of number.
So I tried it out. I invented an operator I called "gorp"
(for no particular reason) which generalized powers. I defined
gorp(2, n) to be n^n. (I am using BASIC's notation for exponents
here since this plain text format doesn't allow much else.)
Then I defined gorp(3, n) to be n^(n^n) since putting the
parentheses the other way, (n^n)^n would reduce to n^(n*n) which
didn't seem as interesting. Of course gorp(4, n) would be
n^(n^(n^n)), and so on. The I defined the inverse, "prog" (gorp
spelled backwards) so that if m = gorp(p, n) then n = prog(p, m).
Here is a table of some values:
n p gorp(p, n)
-- -- -----------
0 2 [undefined]
1 2 1
2 2 4
3 2 27
0 3 [undefined]
1 3 1
2 3 16
3 2 3^9 = 19,683
Clearly this function rises much faster than anything else I knew
of; also, clearly, prog(2, 0) had to be a new kind of number,
since there is no n such that n^n = 0. (Though 0^0 is undefined,
its limit is 1.)
But the math I was being taught took a different turn. Powers
were not generalized to gorp, but to the EXPONENTIAL function,
b^x where b was a constant, and its inverse was the LOGARITHM,
where if a = b^x then log(a) = x (to the base b). Logs are
very useful (and they are undefined at 0, with a limit of
minus infinity) but they weren't the same as prog, nor did
they yield any new types of numbers. For a while it looked like
the imaginary quantity i, and complex number z = a + bi,
were the last new types of numbers to be defined in western
math.
It did seem very curious to me that a funky new irrational
number called "e" was introduced out of nowhere, and used as
the base of the so-called "natural" log, but since e was
approximately 2.7182818284 and not defined in terms of any
roots or other irrationals I knew about, it didn't seem
very "natural" to me. That is, until I learned that if you
take the area under the curve of the inverse function,
y = 1/x, evaluated from the vertical line x=1 to the vertical
line x=k for some number k, the resulting function is log(k)
to the base e! Huh? Where did that come from? (In calculus
notation, the definite integral from 1 to k of 1/x dx is log(k)
to the base e.)
Then one day in about 11th grade an older student told me that
I wasn't supposed to know this yet, but e^(Pi*i) = -1, or
as he glibly said, "e to the Pi i is minus one!" Boy was I
confused. First of all, what did it mean to take a real number
to an imaginary power? How could you multiply e times itself
"i times" anyway? And secondly, e was from logs, Pi was from
circles, and i was from square roots. How could these unrelated
numbers combine in such a goofy way to make something simple like
minus one? I didn't figure that one out for years.
Every now and then I'd ask a mathematician about my
conjecture, and my ideas for gorp and prog. One told me
it sounded a little like Ackermann's function, a super-
quickly growing function which has been studied since 1928.
Interesting, but not helpful (at least to me).
( www.nist.gov/dads/HTML/ackermann.html )
My friend Bill Moulton alerted me to the work on
"hypernumbers" by Charles Muses. He co-edited a book called
"Consciousness and Reality: The New Pivot Point" (1972) which
included his own essay, "Working With the Hypernumber Idea."
( www.amazon.com/exec/obidos/ASIN/038001114X/hip-20 )
Muses claimed that Hamilton's discovery (or was it an invention?)
of quaternions in 1843 represented a new form of imaginary number,
which did not obey the commutative law: a*b did not equal b*a.
(A quaternion contains 4 components, much like a complex number
contains two. They've never made much sense to me, and they
fell out of favor in mathematics early in the 20th century.)
He goes on to describe a series of such new numbers, ultimately
reaching seven of them, counting real and imaginaries as types
one and two. Each new type breaks another law, such as
the associative law, until the seventh does not even obey identity,
i.e., a=a no longer holds. Muses draws spiritual lessons from
all of this, equating the seven types of hypernumbers with seven
stages of the evolution of human consciousness. (I am reminded
of the alchemists, who made a similar association with the stages
of transmuting base metals into gold.) I have studied this paper
extensively over more than a decade but I've never "gotten" it.
By coincidence (or maybe not) Muses has written extensively
on cybernetics. He passed away in 2002, and "Kybernetes: The
International Journal of Systems & Cybernetics" (which he
contributed to frequently) devoted a special issue to him,
Volume 31 Number 7/8 2002, "Special Issue: Charles Muses - in Memoriam."
( matilde.emeraldinsight.com/vl=3034422/cl=67/nw=1/rpsv/cw/www/mcb/0368492x/v31n7/contp1-1.htm )
This work is also related to "Surreal Numbers" (1974) by Donald Knuth.
( www.amazon.com/exec/obidos/ASIN/0201038129/hip-20 )
Both Muses and Knuth introduce the idea that there are positive and
negative forms of zero (!), each of which satisfies the equation
x^2 = 0, which also relates to Kurt Godel's famous Incompleteness
Theorem -- Godel proved that these forms of roots of zero cannot
be definitely proved to exist or not to exist.
But all of these revelations inspired me to go back again and
look at my conjecture. After learning calculus I was able to
determine that for positive x the derivative of y = x^x was
y' = log(x) * x^x, that is equal to 1 when x = 1 (obviously) and
has a limit of 1 when x = 0, and between the two values it forms
an asymmetric "dip" whose minimum is 1/e of all things! When I
learned to manipulate complex numbers I was able to compute
the real and imaginary parts of z^z where z = a + b*i. When
I learned computer programming I was able to draw graphs of the
function, and later do 3D surface plots of the real and imaginary
parts over the complex plane. These are beautiful -- I will share
them in a future C3M if I can find or rewrite the code I used to
generate them -- but I never was able to use these steps to reach
a definition of a new kind of number.
Along the way, though I was able to learn why the mysterious
e^(Pi*i) = -1 is true. It is a specific result of the general
form of Euler's Formula:
e^(i*theta) = cos(theta) + i*sin(theta)
When theta equals Pi, cos(theta) is zero and sin(theta) is one.
This "magic" formula, which like e^(i*Pi) = -1 I learned from
an older student before I was supposed to know about it, is massively
useful. For example, you can use it to find the so-called "trig
identities" which I had to memorize in high school, such as
sin(2*x) = 2*sin(x)*cos(x).
( www.math2.org/math/trig/identities.htm )
I was shown how to derive these "the hard way" but it never stuck
with me. Using Euler's Formula makes it a breeze, and I never
had to memorize another trig identity again. But where did
Euler get this amazing equality? How do you take the imaginary
power of something?
The answer is to be found in the tool known as the Taylor Series.
I studied this in college calculus class, and was able to pass the test,
but never had a clue what the symbols meant. It fell to a physics
professor, David Dorfan, to provide an intuitive understanding.
( scipp.ucsc.edu/personnel/profiles/dorfan.html )
I still remember the day in electromagnetics class that he asked
if any of us could explain the concept. There was silence. We'd
all studied it; calculus was a prerequisite for his class. I
remember him muttering in his charming, clipped accent (British?
South African?) about "what are they teaching you in the math
department," before going to the board and drawing a few figures
and explaining it all in about ten minutes. "How do you think they
compute sines and cosines for the tables?" he implored us. (This
was before affordable scientific calculators, and we used books of
tables of numbers to find the values of trig functions.) "Do you
think they draw giant circles and measure them?"
Here, then, is a brief explanation of the concept which I wrote
for a book I'm currently working on, "A Survival Guide for the
Traveling Techie" (more on that another time):
The Taylor Series allows you to approximate certain well-behaved
functions with simple arithmetic. For a given function of x --
f(x) -- you create a series of terms using x, x squared, x cubed,
and so on, based on knowing the function's value for some single
value of x (often called a) along with it's derivatives at x = a.
You need to able to find its first derivative, second derivative,
third derivative, etc., or in other words: rate of change, rate
of change of rate of change, rate of change of rate of change of
rate of change, etc., or in still other words: slope of the graph,
slope of the graph of the slope of the graph, slope of the graph
of the slope of the graph of the slope of the graph, and so on.
So when you go to predict the function, you use a potentially
infinite expression, but you only add as many terms as you feel
like doing the arithmetic for; if you add up N terms, we say the
result is an Nth order approximation.
Let's look at a simplified example that uses discrete data.
A say we want the value of the function where x = a + 1.
A zeroth order approximation of the function would be zero.
No matter what the value of f(a) and its derivatives are,
who cares, the result will be zero. And in some cases this
is not a bad approximation. It's like assuming nothing
will happen. Sometimes you're right. A first order
approximation would be whatever the function was at x = a.
It will just stay the same. This is true for all constant
functions. It's like assuming the same thing will keep
happening again. Sometime it does. A second order
approximation involves looking at how the function's
value has been changing, say over the interval from a - 1
to a. Call that difference delta (it's not really calculus
without a Greek letter here and there) and say that the
prediction at x = a + 1 is equal to the value at x = a
with delta added.
The actual definition of the series is a summation of an
infinite series involving all the infinite derivatives of f(x).

|
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/t1img684.gif )
(In this equation z is used instead of x and z-sub-0 instead of a.
These are "dummy variables anyway so the names don't matter except
stylistically. The expression f superscript n of z-sub-0 means the nth
derivative of f evaluated at z-sub-0, not the nth power.)
A more thorough treatment of the Taylor Series can be found at
Eric W. Weisstein "Eric Weisstein's World of Mathematics (MathWorld)."
(
mathworld.wolfram.com/TaylorSeries.html )
Dorfan helped me to develop an intuition for the Taylor Series,
but it wasn't until I was out of college for a few years that I
realized its relevance to complex numbers. Again I wanted to make
some progress on my conjecture, I got a small book on "complex
analysis" out of the library and read it. (I've forgotten the title
and author now, but it was standard stuff.) I remember vividly that
I was camping with friends in the piney woods in the Cuyamaca Rancho
State Park in the mountains east of San Diego, at Green Valley Falls
Campground.
(
parks.ca.gov/default.asp?page_id=667 )
[Pointless aside: information on Green Valley Falls can be found
at the gorp (!) web site, named for a type of trail mix.]
I was sitting on a picnic table reading when I came to the
explanation of how e^x and sin(x) are related. A friend of mine
happened upon me and said, "Alan, you've got a huge grin or your
face. Why?" I grappled with how to explain it, and finally just
said, "I just found out the answer to an esoteric question in
math that has bothered me for almost ten years, and it's very
simple and beautiful." But I didn't attempt the explanation --
my friend was not a math type. I will attempt it now, though.
The Taylor Series for both e^x and sin(x) are very easy to
derive, because the derivatives of these functions are so
simple. The derivative of f(x) = e^x is f'(x) = e^x, itself. That's
right, it's its own derivative. So it is its own second derivative
(f''(x) = e^x), third derivative (f'''(x) = e^x), fourth derivative
(f''''(x) = e^x) and so on as well. It is the only function that has
that property, which turns out to be very significant in the
study of Ordinary Differential Equations (ODEs) and dynamical
systems theory using those equations. So in a Taylor expansion
with a = 0, f(a) = e^0 = 1, f'(a) = 1, f''(a) = 1, f'''(a) = 1
all the way up to infinity, and so the terms of the series resolve
to just the rest of the expression, (x - a)/n! where n! is n factorial.
(Both 0! and 1! are defined to be one.) So you can approximate e^x with:
x^0/0! + x^1/1! + x^2/2! + x^3/3! + x^4/4! + x^5/5! + ...
simplified to:
1 + x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + ...
You can see how that n! in the denominator makes the terms
for higher powers drop off really fast. This series converges
very quickly and you can get good quality approximations with
only a few terms.
Now consider f(x) = sin(x). The derivative of a sine is a cosine,
and the derivative of a cosine is a minus sine. So when a = 0,
f(a) = 0 (sine of zero is zero), f'(a) = 1 (cosine of zero is one),
f''(a) = 0 (minus sine of zero is also zero) and f'''(a) = 1
(minus minus cosine of zero is still one) and we're back where we
started. So you can approximate sin(x) with:
0*x^0/0! + x^1/1! + 0*x^2/2! + x^3/3! + 0*x^4/4! + x^5/5! + ...
Those multiplications by zero cause the even terms to vanish
and you're left with:
0 + x + 0 + x^3/6 + 0 + x^5/120 + ...
Likewise cos(x) works out to:
x^0/0! + 0*x^1/1! + x^2/2! + 0*x^3/3! + x^4/4! + 0*x^5/5! + ...
or:
1 + 0 + x^2/2 + 0 + x^4/24 + 0 + ...
The odd terms have dropped out in this case.
Now for the magic: these equations involve x only as whole
number powers: x^1 (i.e., x), x^2, x^3, x^4 and so on. Well,
we know how to take whole number powers of imaginary quantities,
right? By definition i^2 = -1, so we know i^1 = i, i^2 = -1,
i^3 = -1*i, i^4 = 1, and it repeats. So: WE CAN FIND THE VALUES
THE EXPONENTIAL AND TRIG FUNCTIONS WHEN X IS IMAGINARY!
Try it yourself, plug i into each series above and see what you get.
What you'll notice is that e^i gives a series that can be sorted
out, every other term, with a real series for cosine and an
imaginary series for sine. What it ends up showing you is
Euler's Formula:
e^(i*theta) = cos(theta) + i*sin(theta)
No wonder they called him a genius, and no wonder I was grinning
on that picnic table!
Now I know some of you already knew this, and some of you
followed my argument and are now going "Wow!" and some of you
are just plain lost. Sorry about that. One of the ironies
of my own education was that in my junior year of college
I gave up being a math major and dropped a class called "linear
algebra" because it was boring and I just didn't get it. Plus
I had no clue what it was for. I decided instead to pursue an
individual major in "understanding whole systems" with Gregory
Bateson as my adviser. If I'd stayed in that class I would
have learned the above facts in short order. Many years later
I discovered that the most powerful mathematical tools for
studying the general behavior of systems are found in linear
algebra. In other words, of all the math courses at UCSC, it
was the one MOST RELEVANT to what I wanted to study. (I didn't
figure this out for another 10 years.) I blame the way the material
was taught. At that time, 1973, it was a HUGE TABOO in higher
math education to APPLY any of the knowledge or to teach students
how to do so. I came up with this analogy: if they taught mountain
hiking like they taught math, you would be forced to wear blinders
so that you could only see your feet. They wouldn't let you see the
mountain from afar before you climbed it, and they wouldn't let you
see the view from the top -- if you made it.
Another irony: right as I left Santa Cruz, a group of rebels was
forming (in the low-rent Applied Sciences building, isolated from the
mainstream math and science students) which later became known as
the "Chaos Collective," early pioneers of chaos theory, which eventually
was instrumental in healing the rift between pure and applied math
and science in the 1980s. This story is told in "Chaos: making a New
Science" (1987) by James Gleick.
(
www.amazon.com/exec/obidos/ASIN/0140092501/hip-20 )
Okay, fast forward another decade or so, after some background.
My parents were both born and raised in Memphis, Tennessee,
but they transplanted to San Diego, California in 1959, and my
sisters and I grew up there. Our only nearby kinfolk were my
dad's cousin, Robert Scrivener, "Uncle Bob," and his wife Dorothy,
"Aunt Dot." We saw them every Thanksgiving and Christmas, on
birthdays, and other times too, since they were our only relatives
within a thousand miles. Eventually Uncle Bob passed away, and Aunt
Dot married a man named Charles Curtis ("Uncle Charlie"). Though
neither of them was a blood relative we still saw them a few times
a year. Eventually Uncle Charlie passed away, and later so did
Aunt Dot. My parents were executors of her estate, and she left
almost everything to her church. My folks ended up with a pile
of stuff the church didn't want, and so they invited us kids to
pick through it before the rest was tossed in a dumpster. Among
the old National Geographics and Arizona Highways magazines I found
Uncle Charlie's book collection, which divided into three categories:
math puzzles based on number theory (such as Fermat's Last Theorem),
electromagnetic physics texts, and textbooks on electrical circuit
theory. I found myself wishing I'd known he had these interests when
he was alive. Aunt Dot had been a registered nurse and had no
interest that I could see in math or engineering, and it never came
up. I never even knew what Uncle Charlie did for a living.
But his textbooks have enriched me. They proved to be a starter
for a whole collection; several friends saw them on my shelves and
contributed some college texts of their own to my growing
collection, on network theory, control theory, mathematical
modeling, and even cybernetics. Opening up these texts on
occasion I found the math daunting. One concept that I kept
running into -- which I was in complete ignorance of -- was the
Laplace Transform. I thought that maybe some day I would learn
what it was.
In 1988 In began working in the field of scientific computing,
and had to "port" the FORTRAN programs of scientists to a new
model of min-supercomputer (if that isn't an oxymoron, like
"jumbo shrimp.") I ran across the term Laplace Transform often
in the comments to the code. I remember it reminded me of the
slogan, "LA's the Place!" My office was right next to the Los
Angeles Airport (LAX), and every time I passed the little bars
in the departure areas I would see these banners advertising a
drink called a "Green Eyes," the "official" drink of LA, and
the 1984 LA Olympics. Since my wife has green eyes I ended up
trying one. It was a supersweet "candy drink" but I liked it and
ended up buying a set of novelty glasses decorated with green palm
trees, the slogan, "LA's the Place!" and the recipe for the drink:
3/4 oz. (22.5 ml.) Midori
1 oz. (30 ml.) Rum
1/2 oz. (15 ml.) Cream of coconut
1/2 oz. (15 ml.) Lime juice
1 1/2 oz. (45 ml.) Pineapple juice
Blend with crushed ice
(I never met anybody besides the LAX bartenders during the 12 years
I lived in the LA basin who'd heard of the drink, let alone knew it
was the "official" drink of LA.)
That was as close as I ever got to understanding a Laplace Transform
(those Green eyes really got you drunk fast; that was quite a transform!)
until a few weeks ago. I once again cracked one of Uncle Charlie's texts
and ran smack into the loopy L symbol used to represent the Laplace
Transform, and I decided it was time.
I knew who Laplace was. He gave us probability theory pretty
much as we know it today, solving the problem of how to fairly
split up the pot among gamblers in an unfinished, interrupted card
game. From reading "Men of Mathematics" (1937) by E.T. Bell,
(
www.amazon.com/exec/obidos/ASIN/0671628186/hip-20 )
I knew he had lived through the French Revolution and Napoleon's
subsequent rise to power. I knew he had made important contributions
to celestial mechanics. From "A History of Mathematics" (1968) by
Carl B. Boyer,
(
www.amazon.com/exec/obidos/ASIN/0471543977/hip-20 )
I learned he was one of the "three Ls" of 18th century France:
Lagrange, Laplace and Legendre, all of whom lived to ripe old
ages. An on-line biography can be found at the School of Mathematics
and Statistics, University of St. Andrews, Fife, Scotland.
(
www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Laplace.html )
A number of portraits of him are on-line as well.
(
www-groups.dcs.st-and.ac.uk/~history/PictDisplay/Laplace.html )
The significance of his work is discussed in the on-line "Wikipedia."
(
www.wikipedia.org/wiki/Pierre-Simon_Laplace )
To begin my quest, I went to Amazon.com and rather arbitrarily
selected a text, "Complex Variables and the Laplace Transform
for Engineers" (1961) by Wilbur R. LePage, which I ordered.
(
www.amazon.com/exec/obidos/ASIN/0486639266/hip-20 )
When it arrived I was a little disappointed that it was intended
for graduate students who had already learned to solve problems
with the Laplace Transform but wanted a deeper understanding.
But I forged ahead. I did quite quickly get the definition of
the Laplace Transform: if f(t) is defined for all real numbers
greater than or equal to 0, then L(f(t)) is defined as the definite
integral from 0 to infinity of f(t)*e^(-s*t) dt = F(s).
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/l1img987.gif )
Its remarkably simple. I also learned what kinds of problems
it can solve, and how it is used. A classic problem in circuit
theory is: given a circuit made of a capacitor (C), a resistor (R)
and an inductor or coil (L), all in series with an input source of
current with a driving function Va, and measure the output function
Vb across the resistor; find the system function H which expresses
the output in terms of the frequency of the input and the values of
C, R and L. Now replace the capacitor with a whole sub circuit made
of the same type of components and solve again. The Laplace Transform
using this magical property: if you cascade (or "convolve") functions
such as some f(x), g(x) and h(x) into f(g(h(x))), you can find the
Laplace Transform of each function, simply add them up, then apply
the Inverse Laplace Transform and, "Bob's your uncle!" (as they say
in the UK), there's your answer. I was reminded of the power of
logarithms to change multiplication into addition, which is what
makes slide rules work. To clarify here, logs and other operators
work on numbers, to make new numbers, while transforms work on
functions to make new functions. There was a cute comic book to
teach calculus called "Prof. E McSquared's Calculus Primer" (1989),
(
www.amazon.com/exec/obidos/ASIN/0971462402/hip-20 )
that showed transforms as robots that took functions in and
ejected the resulting transformed functions, to illustrate what
derivatives and integrals did. Jim Blinn used a similar technique
in his computer effects for the "Mechanical Universe" TV series.
(
www.pbs.org/als/mech_univ1/ )
But I still didn't have what I wanted. The text I was using
taught me how to plug in the symbols and solve some problems,
and I'm sure there are armies of engineering students out there
who've been trained to do just that. But I didn't have any circuit
design problems to solve; I was after the "deeper understanding"
promised in the introduction and I hadn't gotten it yet.
One clue was that the Laplace Transform is sort of a generalization
of the Fourier Transform. This I was familiar with from my
scientific computing days. Everyone wanted to know how quickly
the new mini-supercomputers could do FFTs -- Fast Fourier
Transforms. I educated myself about this tool, and it was
pretty easy to develop an intuition for the concept. Anyone
who has watched the LED display on a stereo's graphics equalizer
has seen an FFT in action. The input signal, a series of numbers
in the "time domain" (i.e., where the speaker cone is located at
a series of moments in time) is transformed into the "frequency domain"
(what frequencies are present in the signal). This makes sense to
us because it is how our ears work: the little tiny hairs in our
cochlea (inner ear) vibrate nerve endings to tell us what frequencies
are present in the sounds we hear, sort of like how a piano's wires
will vibrate in resonance to sounds in their vicinity.
But here is where I was stuck: the Laplace Transform goes from
the time domain to the "s" domain. Time vanishes and the function
is expressed in terms of a new variable, s, which nobody seemed to
be able to explain.
What I was looking for was an intuition for the meaning
of the equations, so I went to google.com and typed in:
"Laplace Transform" intuition
One web site said s was the "Laplace variable." Oh, great.
another said "The s-domain is simply another way of analyzing
mechanical and electrical systems." I already knew that.
I was offered the clue that s sometimes represents a frequency.
But what is it the rest of the time?
A good summary of the material in my text was at "Eric Weisstein's
World of Mathematics (MathWorld)" at the Wolfram Research web site,
but it didn't attempt to explain s.
(
mathworld.wolfram.com/LaplaceTransform.html )
Finally I happened upon the web site of Duncan K. Foley of the
Department of Economics Graduate Faculty, New School University
in New York.
(
homepage.newschool.edu/~foleyd/ )
In a PDF document entitled "Laplace Transforms"
(
homepage.newschool.edu/~foleyd/GECO6289/laplace.pdf )
he wrote:
From an economic point of view we immediately recognize the
Laplace transform as the present discounted value of the stream
of returns f[t] at the interest rate s. If f[t] is continuous
and differentiable at all t >= 0, then it is possible to recover
f[t] from L[f][s] through the inverse transformation...
This has the economic meaning that if we know the present
discounted value of a stream of returns at every interest rate,
we can recover the whole pattern of the stream of returns.
Ahah! I got it. The "present discounted value" is what an annuity
is worth if you cash it out now. Let's say you go to your accountant
and say, "I won the lottery and they're paying me $10,000 a year, but
I want all the money now. I heard an ad on the radio for these folks
who will give me a settlement now, and they offered me $200,000 cash.
Is this a good deal?" Your accountant says that depends on what
interest rates do, and she gives you a spreadsheet that gives you
a "present discounted value" when you plug in a guess as to what the
interest rate will be. (One simplification -- this model assumes
interest rates are going to hold constant at some rate from tomorrow on.)
In this example, f(t) is the lottery payout function over time,
s is the interest rate, and F(s) is the spreadsheet she gives you.
The amazing thing is, as it says above, "if we know the present
discounted value of a stream of returns at every interest rate,
we can recover the whole pattern of the stream of returns." This
is analogous to the result in Fourier's work, that the time series
can be completely reconstructed from the frequency distribution.
Okay, one more thing for extra credit: if I understand this
correctly, s can be a complex variable. Imagine s = v + w*i,
then v is an "interest rate" and w is a frequency. Taking e^s
gives a combination of exponential growth or decay (e^v)
and harmonic oscillation (e^w*i).
One of the things I learned when I worked on the Support Vector
Machine project in 2001 (see C3M vol. 2 number 3) is that
when you take two strings of numbers (vectors) and "dot product"
them, that is, take (x1, x2, x3, ...) and (y1, y2, y3, ...) and
compute x1*y1 + x2*y2 + x3*y3 + ..., you are measuring the
CORRELATION between the two vectors. In my computer graphics days
I learned to use dot product to find the cosine of the angle between
two 3D vectors of unit length. If they are pointing in the same
direction the cosine is 1, and if they are at right angles the cosine
is zero, so this can be thought of as quantifying how they correlate.
Generalize this to N dimensions, and then to a continuous case.
The Fourier Transform correlates a function with a series of
harmonics; the Laplace Transform correlates it with a combination
of harmonics and exponential curves.
if you have read my "Curriculum for Cybernetics and Systems Theory"
which inspired this e-Zine, you may recall the description and graphs
in the section "Where Cybernetics and Systems Theory Came From"
(
www.well.com/~abs/curriculum.html#From )
Maxwell's analysis of the behavior of governors produced
predictions that combine harmonics and exponential curves,
as the graphs show. For a long time these were thought to be
the only behaviors systems could exhibit.
I still have several bankers boxes filled with issues of
the CoEvoltuion Quarterly and the Whole Earth Review from
the 1970s and 1980s, and I have searched them in vain for the
quote I want to share with you now. Following the publication
of an article by Howard Odum on global energy dynamics, which
included a block diagram of his model of world energy use,
a reader wrote in to say (I'm paraphrasing), "I'm an electronics
engineer, and that diagram looked like an electrical circuit,
and what I know about electrical circuits is they can only do
three things: they can do nothing, they can oscillate, or they
can blow up."
This is an interesting insight, but it is technically not true.
The fourth alternative is they can exhibit chaos, by seeking a
strange attractor. But it only happens in non-linear systems,
which are systems where the Laplace Transform in useless.
Laplace didn't know about chaos because he didn't have a computer.
I have a photocopied page from Kenneth Boulding's "Conflict and Defense:
A General Theory" (1962) -- at least I think that's where it's from;
I neglected to note the book title on the page.
(
www.amazon.com/exec/obidos/ASIN/0819171123/hip-20 )
Wherever it's from, it describes the trajectory of a deterministic
system through a state space, complete with some 2D diagrams,
emphasizing that the path must be unique and so can't fork or cross,
and then asserts:
A moment's consideration will convince you that (since the path
must be unique) a state determined behavior must either converge...
to a fixed state called the 'equilibrium point', or enter a
'behavioral cycle'... Either mode of behavior is called a stable
equilibrium because, unless there is a disturbance which moves the
state point (or alters the subsequent transformation), its behavior
remains invariant.
Again, this is wrong. More than a moment's consideration was
needed to discover that this argument only applies to the 2D case.
In 3 or more dimensions you can find strange attractors
(
sprott.physics.wisc.edu/fractals/animated/nhrisk.gif )
such as Rossler bands

(
sprott.physics.wisc.edu/fractals/animated/ROSSLER.GIF )
Birkhoff Bagels, and other monstrosities. More more such images
see Sprott's Fractal Gallery on-line.
(
sprott.physics.wisc.edu/fractals.htm )
Clearly, 300 years plus of complex analysis using the powerful and
elegant tools bequeathed to us by Laplace have produced generation
after generation of mathematicians, engineers, economists and other
systems experts with intuition lopsidedly biased towards the
linear systems that can be studied analytically. Now with
cheap computers in the hands of new students there is hope that
more "computational experiments" a la Woldfram can run the intuition
the other way.
=======================================================================
newsletter archives:
www.well.com/~abs/Cyb/4.669211660910299067185320382047/
=======================================================================
Privacy Promise: Your email address will never be sold or given to
others. You will receive only the e-Zine C3M unless you opt-in to
receive occasional commercial offers directly from me, Alan Scrivener,
by sending email to abs@well.com with the subject line "opt in" -- you
can always opt out again with the subject line "opt out" -- by default
you are opted out. To cancel the e-Zine entirely send the subject
line "unsubscribe" to me. I receive a commission on everything you
purchase during your session with Amazon.com after following one of my
links, which helps to support my research.
=======================================================================
Copyright 2003 by Alan B. Scrivener