========================================================================
Cybernetics in the 3rd Millennium (C3M) --- Volume 5 Number 2, Mar. 2006
Alan B. Scrivener --- www.well.com/~abs --- mailto:abs@well.com
========================================================================
Even Better Than the Real Thing
Lock your wigs, inflate your shoes,
and prepare yourself for a period of
simulated exhilaration.
-- Firesign Theatre, 1971
"I Think We're All Bozos On This Bus"
( www.amazon.com/exec/obidos/ASIN/B00005T7IT/hip-20 )
Last time's 'zine was quite long -- 16,275 words (a record) for the last
installment and 31,620 for the whole trilogy -- and somewhat tangential
to classical cybernetics (though it did deal with important issues
like the digital revolution, disruptive technology, media ownership
and the democratization of moviemaking). But this time I want to
be more short and to the point, and also to return to fundamentals,
and discuss something at the core of the methodologies of cybernetics
and systems theory: simulation.
A few years ago I got an email that asked this question:
Are there any books (or web pages, etc.) in reference to applied
cybernetics? That is, quantified cybernetic relationships in a
real world application used to solve a problem or accomplish a
goal. Examples outside of the science/engineering world, and
cybernetics applied to business would be of particular interest.
to which I replied:
These days what used to be called cybernetics is usually just
folded into "applied math." In the business world, they used
to call it "operations research" and now they call it
"management science."
Here is the strategy I recommend: use visually programmed simulation
packages. Go to google.com and search for:
easy5 vissim ITI-SIM AMESim
and you'll get links like:
www.idsia.ch/~andrea/simtools.html
which point to vendor web sites. Pick a package you can afford
and use it to build models and play with them. Try to model as
many different types of systems as you can. Then get ahold of real data,
say from an e-commerce sales database, and see if you can build models
that produce similar data.
...
Happy studies!
Since sending this email, I have come to believe it may be the best
advice I have ever given to any of my readers. (I wonder if he
followed it?) So I have decided to expand upon the idea for this issue.
AN OLD KIND OF SCIENCE
Yes, but as a noted scientist it's a bit surprising that
the girl blinded ME with science...
-- Thomas Dolby, 1982
"She Blinded Me With Science" on
"The Golden Age of Wireless" (music CD)
( www.amazon.com/exec/obidos/ASIN/B000007O19/hip-20 )
First, to put things in context, we need a quick review of the
history of the Scientific Method:
- The original methodology is usually attributed to Galileo,
who established this pattern: create a mathematical model
of a natural system (his used simple algebra), make
quantitative measurements, and compare them with the theory.
If the experiments repeatably give different answers
than the theory, modify the theory and repeat.
In this way Galileo was able to establish that a sufficiently
dense body (so that air friction can be ignored), dropped from
slightly above the Earth's surface, will have traveled a
distance of 16*t^2 feet after t seconds have passed. (Here
I write t^2 to indicate t squared, i.e., t*t or t times t,
following the syntax of many computer languages, from BASIC
to Java.) For example, after one second the distance traveled
will be 16*1*1 = 16 feet; after two seconds the distance
traveled will be 16*2*2 = 64 feet; after three seconds it
will be 16*3*3 = 144 feet, and so on. (Note that you don't
need a computer or a 3D graphics system to get these answers.)
Graph this data and you start to get a parabola, or as Thomas
Pynchon called it, "Gravity's Rainbow."
- Isaac Newton made a huge contribution when came up with
the main set of mathematical tools used to model
deterministic systems with a number of interconnected,
continuous (i.e., "smooth when plotted") variables.
Newton's toolbox is built on algebra and geometry, and
includes calculus, so-called "linear algebra" and systems
of Ordinary Differential Equations (ODEs).
- Using his tools Newton was able to prove that -- if you
make some simple assumptions about forces and masses and
gravity -- a single planet orbiting the sun must follow
the shape of an ellipse, a conclusion that matched the
detailed observations of Tycho Brahe, which Kepler had analyzed
and formulated into Kepler's Laws. (Note that you don't need a
computer or a 3D graphics system to get these answers either.)
This much of the story is pretty widely known, representing huge
victories for quantitative science. But the next developments
have been less trumpeted, for they represent defeats.
- It was quickly discovered that Newton's equations did
not yield ready answers when THREE bodies interacting
gravitationally are analyzed. This story is told
in the wonderful paper "A Mathematics for Physiology"
by Alan Garfinkel (1983) which appeared in "The
American Journal for Physiology." Dr. Garfinkel
explains:
The motion of two mass points is then described
by a curve ... the solution curve to this differential
equation for a given set of initial conditions.
Newton's achievement was to show that that this
model yielded Kepler's three laws of planetary motion:
that the planets move in ellipses [&etc]. Before this
derivation, Kepler's Laws had been entirely empirical,
so the explanation that Newton contributed was very
profound. It became the basic paradigm for a rigorous
physical theory: a reduction to a differential equation,
with the hypothesized forces appearing as the right-hand
side of the equation, and the resulting motion of the
system given by the integral curves.
But the beauty of Newton's solution to the two-body
problem did not seem to be extendable. In the typical
cases, even in systems slightly more complex than the
two-body problem, one could write equations based on
first principles, but then it was completely impossible
to say what motions would ensue, because the equations
could not be solved. A classic case was the three-body
problem. This is a more realistic model of the solar
system, because it can take into account the non-negligible
gravitational effects of Jupiter. A great deal of
attention was focused on this problem, because it
expressed the stability of the solar system, a question
that had profound metaphysical, even religious, consequences.
Mathematicians attempted to pose and answer this, some
spurred on by a prize offered by King Oscar of Sweden.
[link added -- ABS]
( www.sciencenews.org/pages/sn_arc99/11_13_99/mathland.htm )
Several false proofs were given (and exposed), but no real
progress was made for 150 years. The situation took a
revolutionary turn with the work of Poincare and Bruns
circa 1890, which showed that the equations of the
three-body problem have no analytic solution. ... They
showed that the usual methods of solving differential
equations could not solve this problem. In addition,
because the write-a-differential-equation-and-solve-it
method had become the normative ideal of an explanation,
the proof that no such solution existed (not just that
people had not found none) had revolutionary consequences:
it represented the defeat of Newton's program.
The revolution was resolved by Poincare. It was his genius
to reevaluate the question and ask what we really wanted
from a mathematical model of nature. Consider the problem
of the stability of the solar system: what are we really
asking for when we are asking if it is stable? To Poincare,
it meant asking whether the orbit of the earth, for
example, was closed, spiraled into the sun, or escaped
into space. He was that the fundamental difference between
the closed orbit and the other two was qualitative: the
closed orbit is essentially a circle, and the other two are
essentially lines. To make this distinction precise required
the invention of a new subject, topology. In the topological
view, only breaks and discontinuities are meaningful;
two figures, such as the ellipse and the circle, which
can be deformed into each other without discontinuities,
are equivalent. However, the circle and the line are not
equivalent, because we must the break the circle somewhere
to map it smoothly and one-to-one onto the line.
Poincare then reposed the fundamental question of dynamics.
No longer was it a request for analytic solutions. Now it
was asking for the qualitative FORMS of motion that might
be expected from a given kind of system. This was the idea
that was to revolutionize dynamics, an idea that requires
a radically different view of dynamics, in which we
imagine it pictorially instead of symbolically.
This definitely made ME go "wow" when I read it. I'd known since
boyhood about the field of mathematics known as topology; I'd read
about it in "The Time-Life Book of Mathematics" (1963) by the
editors of Time-Life --
( go to
ebay.com and search for "Time Life Mathematics" )
and looked at the terrific pictures --

(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/time-life_topology.jpg )
but I didn't know it was INVENTED to solve problems in systems theory.
Elsewhere in the book was a turgid discussion of the unsolved "three
body problem," which I had no clue was connected to topology.

(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/time-life_3body.jpg )
After winning the King Oscar prize Poincare ruminated over what he had
learned by all this, and eventually published his conclusions in
"Science and Method" (1914).
(
www.amazon.com/exec/obidos/ASIN/0486432696/hip-20 )
A more thorough academic study of this event and its consequences
appeared just a decade ago, in "Poincare and the Three-Body Problem
(History of Mathematics, V. 11)" ( book, 1996 ) by June Barrow-Green.
(
www.amazon.com/exec/obidos/ASIN/0821803670/hip-20 )
READ THIS PAPER
A differential equation gives the rule by which the state
of the system determines the changes of state of the system,
which then determine its future evolution.
-- Alan Garfinkel, 1983
"A Mathematics for Physiology" in
"American Journal of Physiology"
Pardon me as I take a short respite from the main exposition to
encourage you to read Dr. Garfinkel's paper. After years of
wishing it was available on the internet, I found it is now
on-line at the web site of the original journal it appeared in
(
www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&list_uids=6624944&dopt=Abstract )
as a PDF document for an $8.00 charge (one day access), and also
temporarily available for free (I'm only telling you what Google
told me) in a separately scanned PDF version
(
www.as.wm.edu/Faculty/DelNegro/cbm/GarfinkelAJP1983.pdf )
at the web site for a class called "Cellular Biophysics and Modeling"
(
www.as.wm.edu/Faculty/DelNegro/cbm/cbm.html )
taught by Christopher Del Negro
(
www.as.wm.edu/Faculty/DelNegro.html )
at the College of William and Mary Dept. of Applied Sciences.
(
www.as.wm.edu )
A check of Dr. Del Negro's CV shows that he obtained his PhD in
Physiological Sciences in 1998 from UCLA, where Dr. Garfinkel teaches,
(
www.physci.ucla.edu/physcifacultyindiv.php?FacultyKey=965 )
(
www.cardiology.med.ucla.edu/faculty/garfinkel.htm )
(it's a sure bet Del Negro was Garfinkel's student there) and is
now building his expertise in the area of chaos and respiration,
leading him to study sleep apnea -- which is coincidentally the field
I have worked in for the last year, at ResMed Corp.
(
resmed.com )
I first ran across Dr. Garfinkel's paper in the late 1980s, when
I worked for Stardent Computer and he was a customer, using his
new supercomputer to analyze cardiac chaos. I ended up handing
out photocopies of "A Mathematics for Physiology" to other Stardent
customers, acting as a "pollinating bee" for his ideas (or a
"supernode" in network theory).
Overjoyed as I am that it is now available electronically, I urge
you now to take a respite from this 'zine and read the paper --
at least the first five pages. I'll wait.
MUDDLING THROUGH
Is dis a system?
-- "Mr. Natural"
(
www.toonopedia.com/natural.htm )
a character created by underground cartoonist R. Crumb
(
www.toonopedia.com/crumb.htm )
Welcome back.
Stymied by the three-body problem and other complications,
systems theory stalled for a while. Poincare's topology
solved some simple problems that were intractable under
analysis, but did not offer a general program for proceeding
with many other real world problems. In assembling his writings
on a generalized theory systems, Ludwig Von Bertalanffy wrote
in "General System Theory" (book, 1968)
(
www.amazon.com/exec/obidos/ASIN/0807604534/hip-20 )
about the problems of using Newton's paradigm:
Sets of simultaneous differential equations as a way to "model"
or define a system are, if linear, tiresome to solve in the
case of a few variables; if non-linear, they are unsolvable except
in special cases.
and then provides a rather alarming table of how things really are.
(
www.well.com/~abs/equations.html )
In the same year, ecological cyberneticist Ramon Margalef wrote in
"Perspectives in Ecological Theory"
(
www.amazon.com/exec/obidos/ASIN/0226505065/hip-20 )
Almost inadvertently we have been shifting from the consideration
of elementary relations in the ecosystem, like the response of
a population to an environmental change or the interaction between
a predator and its prey, to elementary cybernetic feedback loops
and to the multiplicity and organization of a great number of such
feedback loops. Almost everyone would agree it would be difficult,
but theoretically feasible, to write down the interactions between
two species, or possibly three, according to the equations suggested
by Volterra and Lotka. This can be done in ordinary differential
form as expressions, or in the more fashionable cybernetic form.
But it seems a hopeless task to deal with the actual systems;
first because they are so much too complex, and second because we
need to know many parameters which are unknown.
When major portions of this book were reprinted in the Summer 1975
issue of the "CoEvolution Quarterly," a diagram was included that
sheds light on cybernetic relationships between predator and prey levels.
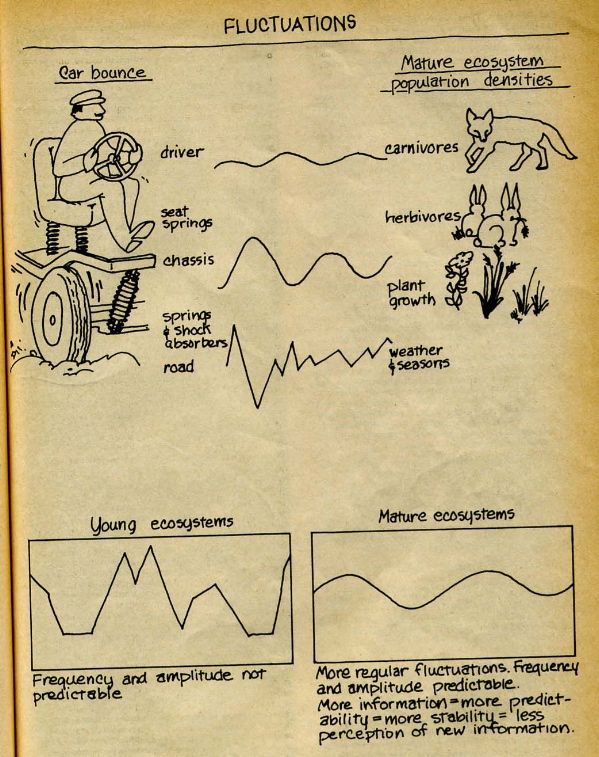
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/margalef.jpg )
Both authors, Von Bertalanffy and Margalef, end up concluding that
systems must be studied, even if the tools are inadequate, and both
go on to advocate that HEURISTICS be used as stop-gap measures, such
as simplifications, analogies, intuition, etc., nibbling on the
corners of problems that can't be solved outright.
WHAT'S THE FREQUENCY, NORBERT?
When I came to M.I.T. around 1920, the general mode of putting
the questions concerning non-linear apparatus was to look for a
direct extension of the notion of impedance which would cover
linear as well as non-linear systems. The result was that the
study of non-linear electrical engineering was getting into a
state comparable with that of the last stages of the Ptolemaic
system of astronomy, in which epicycle was piled on epicycle,
correction upon correction, until a vast patchwork structure
ultimately broke down under its own weight.
-- Norbert Wiener, 1961
"Cybernetics, Second Edition"
(
www.amazon.com/exec/obidos/ASIN/026273009X/hip-20 )
Perhaps the most heroic efforts against the unsolvability of general
systems theory was the prodigy genius Norbert Wiener. Recently an
informative biography of him was published, "Dark Hero Of The
Information Age: In Search of Norbert Wiener The Father of Cybernetics"
(book, 2004) by Flo Conway and Jim Siegelman.
(
www.amazon.com/exec/obidos/ASIN/0738203688/hip-20 )
From it I learned that, sitting at MIT and traveling to collaborate
with a long, impressive list, Wiener had his hand in the rebirth of
Fourier and Laplace Transform techniques, the framing of the Uncertainty
Principle in quantum physics, the selection of base 2 for use in
information measure (definition of a bit) and processing (binary
computers), and some other cool stuff I don't remember right now,
but he spent quite a bit of his time trying to beat nonlinearity,
hurling himself at the door over and over again trying to get it
to open. (He noticed that random functions survived some nonlinear
transforms the way sine and cosine survived adding 360 degrees
to angles in linear equations, and thought he was on to something.
As it turned out, not so much.)
At the time it seemed Wiener's most promising approach was the
so-called frequency methods, which used Fourier's Integral
and related tools to spread data out on a "Procrustean Bed"
of frequency analysis (sort of like today's Graphic Equalizers
and Spectrum Analyzers in audio systems)
(
www.audiofilesland.com/company/axis-software-company/axis-spectrum-analyzer.html )
and characterize it by frequency distributions and how they evolve
over time. (Sort of like studying motors by listening to the sounds
they make.)
One of his more fruitful approaches was to use analog computers, and
when they proved unbuildable for some nonlinear problems he proposed
that they needed to start building DIGITAL computers and using them
to SIMULATE nonlinear systems. What he wanted to do was to use the
oldest method for calculating values from differential equations,
Euler's Method, also known as Euler integration, which just starts
with the initial conditions and approximates the evolution of the
system in small steps, adding tiny amounts to each state variable
based on the change equations.
(
en.wikipedia.org/wiki/Euler%27s_method )
It is pretty effective, but takes a huge amount of computation.
And more recent refinements that estimate and correct for error due
to the "chunky" time steps, such as the Runga-Cutta method, are even
more accurate and require even more computation.
MAYBE IF WE TRIED SOME KIND OF 'DIGITAL' COMPUTER
"I been in the trade forever. Way back. Before the war,
before there was any matrix, or anyway before people knew
there was one." He was looking at Bobby now. "I got a pair
of shoes older than you are, so what the #### should I
expect you to know? There were cowboys [i.e., system crackers]
ever since there were computers. They built the first
computers to crack German ice [ICE = Intrusion Countermeasure
Electronics]. Right? Codebreakers. So there was ice
before computers, you wanna look at it that way."
He lit his fifteenth cigarette of the evening, and smoke
began to fill the white room.
-- William Gibson, 1987
"Count Zero" (sci-fi novel)
(
www.amazon.com/exec/obidos/ASIN/0441117732/hip-20 )
(
project.cyberpunk.ru/lib/count_zero/ )
There are three main "creation myths" associated with computers.
Retired admirals still like to tell each other that these oversized
adding machines were funded to crank out ballistics tables faster,
so the sailors could fire their 16" guns in any wind conditions.
There may still be some veterans of the US and British codebreaking
efforts in World War Two, who chuckle over how everyone else thought
the "Turing Machine" was a mathematical fiction, but Alan Turing built
one at Bletchley Park to crack the German "Enigma" code.
The third group was the practitioners of systems theory -- and applied
physics -- who wanted to use the new high-speed computers to simulate
systems of ordinary differential equations.
I've described in a previous 'zine the "Fermi-Pasta-Ulam problem"
which was an early simulation of a nonlinear system done at Los Alamos,
in C3M Volume 2 Number 1, Jan. 2003, "Why I Think Wolfram Is Right".
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/c3m_0201.txt )
They were the pioneers who helped establish a new "simulation paradigm"
after World War II. By the time I was in the supercomputer biz in 1988
I found people using simulations to study diffusion of ground water (for
Yucca Mountain studies), sloshing of fluids (in missile fuel tanks),
cracking of metal at high heat and pressure (in rocket nozzles), and
diffusion of heat (in a reactor).
May years ago at some aerospace company I saw a picture that summarized
the paradigm. I was able to get a photocopy, and I've scanned it for you:
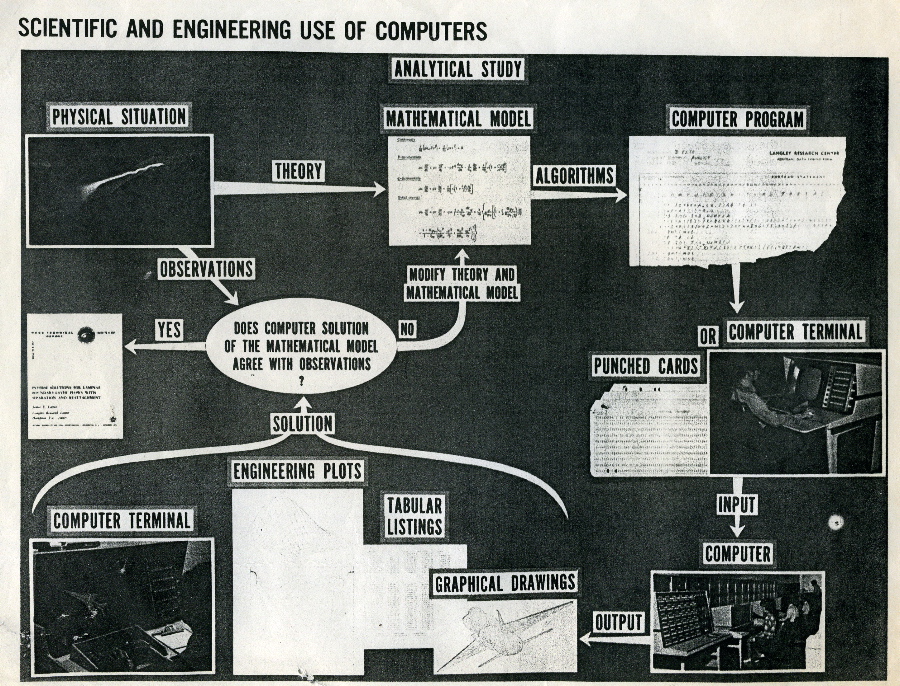
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/scientific.jpg )
And they would have probably gone on indefinitely building better bombs
this way except that some funky things kept happening, like turbulence.
THE ONSET OF CHAOS
The simple linear feedbacks, the study of which was so
important in awakening scientists to the role of cybernetic
study, now are seen to be far less simple and far less
linear than they appeared at first view.
-- Norbert Wiener, 1961
"Cybernetics, Second Edition"
(
www.amazon.com/exec/obidos/ASIN/026273009X/hip-20 )
One of things that seemed to amaze everybody when chaos showed up
in the 1980s is why they never noticed it before. In each field
the evidence had been piling up and was being ignored. Weather
patterns, dripping faucets, epileptic seizures, lemming populations --
all had chaotic modes.
When people tell me they want to learn about chaos I sometimes suggest
they start at a casino. Rolling dice, shuffling cards, churning Keno
balls in a fishbowl -- all are examples of chaos being used to generate
apparent randomness.
Of course chaos would never have been discovered without computers.
We were perfectly willing to blame erratic events on "noise" and
such until computers showed us that deterministic, non-periodic
systems could exist in our mathematical models.
The tale is still told best in "Chaos -- The Making of New Science"
(book, 1988) by James Gleick,
(
www.amazon.com/exec/obidos/ASIN/0140092501/hip-20 )
which showed up at about the same time as my entry into the
supercomputer world. The university research centers, aerospace
companies and national labs I had as customers were all abuzz about
this stuff.
Everyone knew the oft-told tale of Lorenz's discovery of the
attractor that bears his name, and the so-called "Butterfly Effect"
it illustrated.
(
en.wikipedia.org/wiki/Lorenz_attractor )
One well-researched web site, "Hypertextbook" gives a detailed account.
(
hypertextbook.com/chaos/21.shtml )
The article describes the process Lorenz went through trying to
simplify a set of equations that showed instabilities in atmospheric
convection. He finally reduced to only three differential equations.
Although greatly simplified, we have here a model that is still
impossible to solve analytically and tedious to solve numerically.
One that would require an army of graduate students scribbling on
hundreds of pages of paper working around the clock. It probably
wouldn't have been solved in 1960 if it weren't for the fact that
Lorenz had something better than an army of human computers -- the
improbably named Royal McBee -- an early electronic computer whose
vacuum tubes could perform sixty multiplications a second, round
the clock, without taking a break or asking for time off. The Royal
McBee made it possible to do numerical calculations that would have
been cruel and unusual punishment to the human calculators. One
could configure it in the morning and let it run for hours or days,
printing out solutions for later analysis. This is how Lorenz
discovered chaos.
In the course of doing this I wanted to examine some of the
solutions in more detail. I had a small computer in my office
then so I typed in some of the intermediate conditions which
the computer had printed out as new initial conditions to
start another computation and then went out for awhile. When
I came back I found that the solution was not the same as the
one I had before. The computer was behaving differently. I
suspected computer trouble at first. But I soon found that
the reason was that the numbers I had typed in were not the
same as the original ones. These were rounded off numbers.
And the small difference between something retained to six
decimal places and rounded off to three had amplified in the
course of two months of simulated weather until the difference
was as big as the signal itself. And to me this implied that
if the real atmosphere behaved in this method then we simply
couldn't make forecasts two months ahead. The small errors in
observation would amplify until they became large.
In order to conserve paper, the computer was instructed to round
the solutions before printing them. Thus, a solution like 0.506127
was printed as 0.506. Even in 1960 computers gave answers with more
significant digits than were required for most problems. An error of
one part in four thousand should hardly have been significant.
Tolerances aren't anywhere near this tight in construction or
manufacturing or life in general. If you built your home using a
meter stick that was 999.7 millimeters long would your house
collapse? Would it be askew? Would you ever notice anything was
wrong with it?
When it comes to the weather, the answer to that last question was
"yes." After enough time had elapsed, the tiny error introduced by
dropping the digits after the thousandths place became an error as
large as the range of possible solutions to the system. Lorenz
called this the Butterfly Effect.
This watershed event showed most of the enduring features of chaos:
deterministic behavior without periodic behavior, sensitive dependence
on initial conditions, and hidden beauty with fractal properties.
The best way I have found to appreciate the Lorenz Attractor is
to play with a simulation. Several are on-line.
(
www.geom.uiuc.edu/java/Lorenz )
(
www.falstad.com/mathphysics.html )
The best way to learn about chaos in detail, in my opinion is
to study the so-called "chaos comics" by Abraham & Shaw, "Dynamics:
The Geometry of Behavior" (multi-volume book, 1982).
(
www.amazon.com/exec/obidos/ASIN/0201567172/hip-20 )
Its hand-drawn color diagrams of a whole rogues gallery of strange
attractors help develop an intuition for just how mind-bogglingly
weird the pure mathematics of systems theory can be.
A SIMPLIFIED EXAMPLE FOR PEDAGOGIC PURPOSES
It's so simple, so very simple,
that only a child can do it.
-- Tom Lehrer, 1964
"New Math" (novelty song)
on "That Was the Year That Was"
(
www.amazon.com/exec/obidos/ASIN/B000002KO7/hip-20 )
(
www.sing365.com/music/lyric.nsf/SongUnid/EE27EF26A4F581BE48256A7D002575E1 )
Tell me honestly, how many of you stumbled over the word
"pedagogic" above? Let's see a show of hands. You can look
it up in Wikipedia:
(
en.wikipedia.org/wiki/Pedagogic )
One reason kids are such great learners is they don't mind feeling
stupid so much; they just go right on learning anyway.
I firmly believe you could teach kids systems theory all the way up
to ODEs without much arithmetic or algebra, and with no proofs at all,
but WITH interactive simulation software that works from block diagrams
and produces graphs and animations of the system behaviors.
But meanwhile, I also have a very simple example that yields
surprisingly subtle insights if you think about it enough.
So reach into yourself and invite your inner child to ponder this:
A Very Simple Game
Have you ever seen the prank where you hand someone a card that
says "how to keep an idiot occupied for hours (see over)"
printed on both sides? Well this idiotic game is like that,
only it's played on a checkerboard. Each square is numbered 1
to 64. On each square is a small card thats says something like
"go to square 18" or some other number from 1 to 64.
In each round of the game, there is a different set of
cards on the checkerboard.
You play by placing your marker (perhaps a miniature Empire
State Building) on one of the squares (called the 'current
state of the system'), and then following the instructions on
the cards one after another.
Imagine in one round every card says "go to square 1" and so
clearly you have one square that you always end up on, and then
you stay there. In systems theory is this is called an "attractor."
Imagine if in another round the left half of the board
pointed to square 1, and the right half pointed to
the opposite corner, square 64. Now the state space is
divided into two "basins" each with its own attractor.
Or imagine if each square pointed to the one above or to the right
or both, until all jumps ended up on the top or right side.
The square in the lower left corner with so many jumps leading
away from its its vicinity is called a "repellor."
Or imagine that all squares in the interior point to an edge
square, and all the edge squares are joined in a chain that
goes around the perimeter clockwise (i.e., on the bottom row
each square points to the one to the left, meanwhile on the
left edge each square points to the one above it, and so on).
Now we have an "orbit" which in this case is also an attractor.
It is amazing the number of distinctions that can be drawn by studying
this idiotic little game.
This approach is largely the one in Ross Ashby's classic "An Introduction
to Cybernetics" (book 1956)
(
www.amazon.com/exec/obidos/ASIN/0416683002/hip-20 )
which is back in print and also free on-line.
(
pcp.lanl.gov/ASHBBOOK.html )
And unlike me, he continues the analogy while generalizing to
the continuum (infinitely many states) thereby deriving the whole
of cybernetics.
HOW ABOUT A REAL-WORLD PROBLEM?
Gentlemen! You can't fight in here.
This is the War Room!
-- Stanley Kubrick, Terry Southern and Peter George, 1964
screenplay for "Dr. Strangelove" (movie)
(
www.amazon.com/exec/obidos/ASIN/B0002XNSY0/hip-20 )
The deep and thought-provoking museum exhibit and book of the same
name, "A Computer Perspective" (1983) by the incomparable Charles
and Ray Eames,
(
www.amazon.com/exec/obidos/ASIN/0674156269/hip-20 )
tells the story of a pioneer of applied systems theory, Lewis
Fry Richardson. The founder of scientific weather prediction,
Richardson's equations for the behavior of air under all conditions
of pressure, flow, moisture, etc., are still used today.
His 1922 text "Weather Prediction by Numerical Process"
(
www.amazon.com/exec/obidos/ASIN/0521680441/hip-20 )
is still a classic. (This picture taken from that book
resembles my checkerboard analogy.)
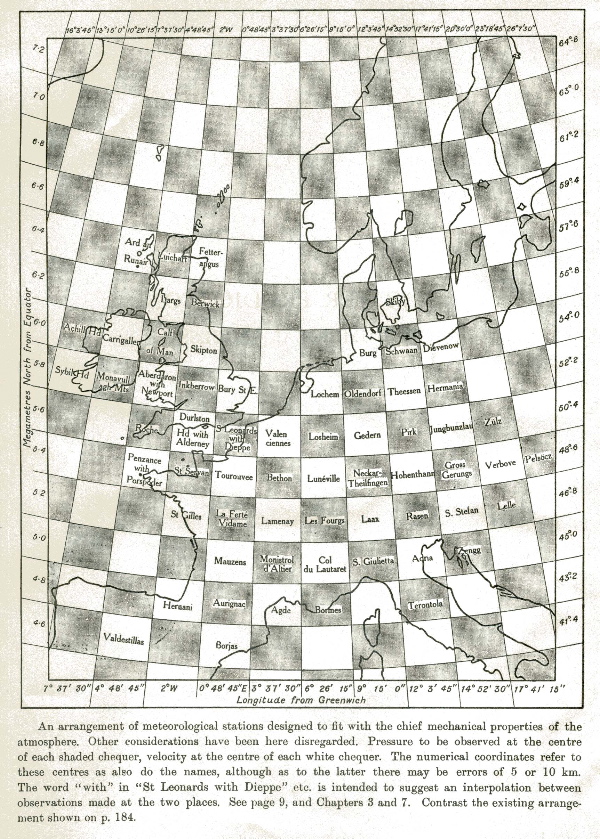
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/richardson.jpg )
But as the Eames explained:
Richardson was a Quaker and conscientious objector. His wife
recalled, "There came a time of heartbreak when those most
interested in his 'upper air' researches proved to be the
'poison gas' experts. Lewis stopped his meteorology researches,
destroying such as had not been published. What this cost him
none will ever know!"
He devoted the rest of his life to the mathematical study of the
causes of war, publishing several books on the subject and single-
handedly founding quantitative sociology. His "Arms and Insecurity"
(written in 1953 -- the year of his death -- and published in 1960)
(
www.amazon.com/exec/obidos/ASIN/0835703789/hip-20 )
presents a model of an arms race between two nations. Let's map
it on to the checkerboard game. Say that the lower left corner
(square 1) represents each nation spending nothing on arms.
Then motion to the right represents nation A spending more on arms,
in increments of 2% of its Gross National Product (GNP), while
moving up represents nation B spending more on arms. Let's assume
the nations behave in a perfectly symmetrical manner. Each time
step will be a year, a typical government funding cycle.
Now you have to ask yourself, if you were Minister of Finance for
nation A, and you were spending 6% of your GNP on arms while your
hostile neighbor nation B spent 10% of their GNP, what would
do next year? Then you have to do it again for every combination
of A and B's spending on the board.
It quickly become obvious that for "reasonable" human responses to
each scenario you end up with a system in which the state moves
up and to the right, in an unending arms race (at least until you
run out of checkerboard. I think the U.S. and its allies won the
Cold War and beat the U.S.S.R. because they ran out of checkerboard
first.) But up until that time things were pretty dicey. Richardson
quoted Sir Edward Grey, British Foreign Secretary a the start of
World War I:
The increase of armaments that is intended in each nation
to produce consciousness of strength, and a sense of security,
does not produce these effects.
Our little checkerboard model helps us understand why.
SYMBOLS VS. PICTURES
Alice was beginning to get very tired of sitting
by her sister on the bank, and of having nothing
to do: once or twice she had peeped into the book
her sister was reading, but it had no pictures or
conversations in it, "and what is the use of a book,"
thought Alice, "without pictures or conversations?"
-- Lewis Carroll, 1865
"Alice's Adventure in Wonderland"
(
www.amazon.com/exec/obidos/ASIN/0393048470/hip-20 )
Drawing pictures of the world-lines of systems in a state space didn't
used to be so popular, you know. Many of the great mathematicians of
the last 300 years have taken a dim view of "visualizing" analytic
results, especially among the French masters, thinking of geometry
as a crutch for the weak. (Ironically, this is even true of
Poincare's topology -- "real" mathematicians work it all out
with symbols alone!)
As R. Buckminster Fuller explained in the essay "Prevailing Conditions
in the Arts" in his book "Utopia or Oblivion" (1970),
(
www.amazon.com/exec/obidos/ASIN/0553028839/hip-20 )
scientists stopped using pictures so much around the time they
began exploring electromagnetic forces, and ultimately the
rather erudite equations of James Clerk Maxwell.
(
en.wikipedia.org/wiki/Maxwell's_equations )
As Bucky describes it:
They found themselves getting on very well without seeing what
was going on. It was during some of these early experiments on
energy behaviors that a fourth-power relationship was manifest.
The equations contained a fourth power x^4. You can make a model
of x^3, e.g. a cube, and you can make a model of x^2 (X to the
second power) and call it a square, and a model of x^1 and call
it a line; but you could not make a geometric model of x to the
fourth power. The consequences of this unmodellable fourth-power
. . . are tied up with other events. At the same historical
period literary men were trying to explain the new invisible
electrical energy, which could do yesterday's tasks with new
and miraculous ease, to their scholarly readers and the public
in general. They began to use visually familiar analogies to
explain the invisible behaviors. The concept of a current of
water running through a pipe as analogous to electricity running
through wires was employed by the nonscientific writers. The
scientists didn't like that at all, because electricity really
doesn't behave as water. Electricity 'ran' uphill just as
easily as 'downhill' (but it did not really 'run'). The scientists
felt that analogies were misleading and they disliked them.
When the experiments that showed a fourth power relationship
occurred, the scientists said 'Well, up to this time we have felt
that visual models were legitimate (though not always easy to
formulate), but now, inasmuch as we can't make a fourth-power
energy-relationship model, the validity of the heretofore accepted
generalized law of models is broken. From now on physically
conceptual models are all suspect. We're going to work now
entirely in terms of abstract, "empty set" mathematical expressions.'
Their invisible procedures thenceforth to this day [~1970] have a
counterpart in modern air transport and night fighter flying --
which is conductible and is usually conducted 'on instruments.'
When you qualify for instrument flight you are to fly in fog and
night without seeing any terrain. You get on very well, and arrive
where you want on instruments. Scientists went 'on instruments'
about 1875 -- almost entirely. By the time I went to school at
the turn of the century we were taught about instruments and
equations and how to conduct experiments. We were taught that the
forth dimension was just 'ha ha' -- you could never do anything
about it.
I remember reading a story, which I can't seem to find corroboration
for on the web, about John von Neumann defending his design for
a digital computer (at the Institute for Advanced Studies in Princeton)
against critics. They said if you had a high-speed computer
it would do calculations so fast that you couldn't print them out
at that speed, and even if you could nobody could read them that fast,
so what was the use? Von Neumann replied that he could hook the
computer up to an oscilloscope and WATCH the computations proceed.
(And he did.)
But of course that oscilloscope is mainly used to plot
one dimensional data changing over time.
(I think sometimes that after Galileo revolutionized astronomy
in 1610 using a telescope to discover the moons of Jupiter, then
Pasteur revolutionized biology 1862 using a microscope to discover
disease germs, and then Janssen revolutionized chemistry in 1868
using a spectroscope to discover Helium, the cybernetics group
were trying valiantly to discover something revolutionary with
the oscilloscope.)
We are fortunate that the Lorenz Attractor is only three dimensional,
and so people can look at it. If it had been 4D there might not
have been a Chaos Revolution in the 1980s -- it might have been
too hard to "get."
But the Lorenz Attractor just a pedagogic example, simplified
so that we CAN see it. The real systems we have to deal with
are very, very high dimension. Newton's sun-and-planet system
that produces the elliptical orbit (and all of the conic sections)
has eight equations and eight variables -- that's the simple,
solvable textbook example.
This lead us to something I call the "Cyberspace Fallacy."
We've had ideas developed in science fiction about direct-brain
computer interfaces into some kind of Computer Graphic representation
of the thing-that-the-Internet-evolves-into.
In "True Names" (sci-fi short story, 1980) by Vernor Vinge,
reprinted in "True Names and the Opening of the Cyberspace Frontier"
(
www.amazon.com/exec/obidos/ASIN/0312862075/hip-20 )
(
home.comcast.net/~kngjon/truename/truename.html )
The imagery of this interface is deliberately vague, suggesting
some kind of high-dimensional direct-knowledge, or "grokking"
of the data.
They drifted out of the arpa "vault" into the larger data
spaces that were the Department of Justice files. He could
see that there was nothing hidden from them; random archive
retrievals were all being honored and with a speed that would
have made deception impossible. They had subpoena power and
clearances and more.
* * * * * *
"Look around you. If we were warlocks before, we are gods now.
Look!" Without letting the center of their attention wander, the
two followed his gaze. As before, the myriad aspects of the
lives of billions spread out before them. But now, many things
were changed. In their struggle, the three had usurped virtually
all of the connected processing power of the human race. Video
and phone communications were frozen. The public data bases had
lasted long enough to notice that something had gone terribly,
terribly wrong. Their last headlines, generated a second before
the climax of the battle, were huge banners announcing GREATEST
DATA OUTAGE OF ALL TIME.
Later, William Gibson sharpened the idea, and named it "cyberspace,"
in "Neuromancer" (sci-fi novel, 1986).
(
www.amazon.com/exec/obidos/ASIN/0441569595/hip-20 )
A cowboy [cracker] is using a direct-brain-interface to defeat
a company's ICE in this vivid scene:
Case's virus had bored a window through the library's command
ice. He punched himself through and found an infinite
blue space ranged with color-coded spheres strung on a tight
grid of pale blue neon. In the non space of the matrix, the interior
of a given data construct possessed unlimited subjective dimension;
a child's toy calculator, accessed through Case's Sendai, would
have presented limitless gulfs of nothingness hung with a few
basic commands. Case began to key the sequence the Finn had
purchased from a mid-echelon sarariman with severe drug problems.
He began to glide through the spheres as if he were on invisible
tracks.
Here. This one.
Punching his way into the sphere, chill blue neon vault above
him starless and smooth as frosted glass, he triggered a sub-
program that effected certain alterations in the core custodial
commands.
Out now. Reversing smoothly, the virus reknitting the fabric
of the window.
Done.
Cool as jazz, for sure, but here's the rub. The problem isn't
in visualizing low-dimensional data like router topologies
(how the servers are wired together) but high-dimensional data
like traffic load over time at every node, broken down by data
type (voice, video, machine instructions, text, etc.). The problem
is two-fold: how to REPRESENT the high-dimensional data, which is
pretty darned tricky, and then how to TRAIN the users to "read"
the data, which they surely will not naturally understand
at first viewing.
BEYOND LIES ANOTHER DIMENSION
Electronic man has no physical body.
-- Marshall McLuhan
I was fortunate in Junior High School to have the same great math
teacher in 7th and 8th grade: Aubrey Dunne, who is still my friend
40 years later. He recognized my budding curiosity about math,
and recommended I read the book "One Two Three... Infinity: Facts
and Speculations of Science" (1947) by George Gamow.
(
www.amazon.com/exec/obidos/ASIN/0486256642/hip-20 )
One of the things this book tried to explain was the 4th dimension,
using various tricks such as the "tesseract" figure and a "2-worms-
in-the-apple" analogy.
I worked on the problem myself, as a kid and later as an adult.
One of my explorations is explored in the paper "Visualizing 4D
Hypercube Data By Mapping Onto a 3D Tesseract" (1996)
by Alan B. Scrivener
(
www.well.com/~abs/SIGGRAPH96/4Dtess.html )
submitted for presentation as a Research Paper at the ACM/SIGGRAPH
'96 Conference held August 4-9, 1996 in New Orleans, Louisiana ,
but not accepted. (They pointed out I was only exploring the eight
cubes that form the 4-D "faces" of the hypercube. But I could solve
that by slicing over time!)
I later discovered the work of Alfred Inselberg, as I reported in
C3M June 2003, "Steers, Beers and the Nth Dimension."
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/c3m_0206.txt )
Inselberg finally has a web site with some of his research posted.
(
www.math.tau.ac.il/~aiisreal )
Click on "Images" for the good stuff.
I have previously compared his "parallel coordinates" to the "sick
bay" readout on TV's original "Star Trek" series.
(
www.amazon.com/exec/obidos/ASIN/B0002JJBZY/hip-20 )

(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/SG2002/sickscan.jpg )
But the two best methods I have happened upon for visualizing higher
dimensions I call the "N-Dimensional Tic Tac Toe" and "N-Dimensional
Elevator" metaphors.
In "N-Dimensional Tic Tac Toe" I like to play 4-in-a-row because otherwise
the center square is a super-duper square, and the first player has a
huge advantage. You know how to draw a 2D game. To make a 3D game just
draw 4 2D games in a row, separated by a little space. Those are the
4 slices in the third dimension, like the floor plan to a low-rise building.
Then duplicate this 4-in-a-row pattern of 2D game fields three more times
below, making a 2D array of 2D arrays. There's your 4D game. This will
easily fit on an 8.5x11 inch sheet of paper, and you can draw it and
photocopy it to make playing fields for real 4D tick-tack-toe games.
Great for older kids on car trips. A win is (1,1,1,1),(1,1,1,2),(1,1,1,3),
(1,1,1,4) for example, or (1,4,4,1),(2,3,3,1),(3,2,2,1),(4,1,1,1).
Each independent coordinate has to stay the same or rise/fall by a unit
with each X or O position to form 4 in a 4D row.
Now, you can make a row of 4 of these pages, and get a 5D game,
or make a 4x4 array of them on the floor, and get a 6D game, and so
on. You may need some sheets of poster board for the next steps.
The other metaphor is the "N-Dimensional Elevator" which is much simpler.
Let's say you're in a 13-story 7-dimensional building full of large,
windowless apartments. Each apartment is only 3D, so you'll feel at
home, and the elevator is 3D so humans can ride in it, but you get in
and there are 7 vertical columns of buttons, one for each dimension,
and each column has 13 buttons for the 13 "floors" in that dimension.
Like a Chinese menu, you select one from each column, and then the
elevator takes you there. Anything you leave in an apartment you will
find there later by pushing the same buttons. But if you leave a barking
dog the neighbors in 14 directions (instead of 6 directions in a 3D
building) might complain.
After much thought I have concluded that if a Turing Machine can simulate
a system of any dimensionality (and it can, and so can any computer)
then dimensions don't matter so much in finite systems. The checkerboard
model I described previously sometimes acted 2D and sometimes 1D, but
because in the most general case any state could lead to any other, you
COULD argue that it's an INFINITE-dimensional system. Only by REMOVING
transitions can you constrain it to act 2D, as in the model of the
Richardson arms race.
Something else I've been pondering is this: if we found chaos by going
from 2D to 3D, what is waiting for us to discover in going from 101
dimensions to 102? (Not to mention all the steps along the way.)
I fear that these are the sorts of questions that only Wolfram's method
can answer: simulate all possibilities and look at the results.
INSTRUCTIONS PER SECOND
SCENE: Jobs and Woz walking up stairs carrying a box.
WHOOPIE: "Believing in things and making them happen has
always been the California way. Soon a new gold rush was
taking place in Northern California."
JOBS (as Woz trips): "Watch it Woz...
SCENE: Room of people crowded at the table looking at the computer.
JOBS (arms open): "Well, here it is. The first personal computer."
CROWD: Wow / Alright / Clapping...
WOZ: "We could sell like a dozen of these!"
JOBS: "Whadaya talkin' about? We're gonna sell one to
everyone on the planet."
-- "Golden Dreams" (theme park show, 2001)
at Disney's California Adventure, Anaheim, California
(
www.disneyfans.com/articles/2001/03-01-01_California_Apple.htm )
(
en.wikipedia.org/wiki/Golden_Dreams )
Of course, Steve Jobs is right; he IS going to sell one to
everyone on the planet. If you count imbedded systems computers
now outnumber people in the U.S.A.
The supply of cheap computers in the 1980s made possible the switch
from frequency methods to state space methods, and the resulting
renaissance of applied systems simulation.
The story is told in "Control Systems Design" (1986) by Bernard Friedland
[revised as "Advanced Control Systems Design" (1995)].
(
www.amazon.com/exec/obidos/ASIN/0130140104/hip-20 )
This is the text I used when I studied control theory at UCLA:
The history of control theory can be conveniently divided into
three periods. The first, starting in prehistory and ending in
the early 1940s, may be termed the PRIMITIVE period. This was
followed by a CLASSICAL period, lasting scarcely 20 years, and
finally came the MODERN period which includes the content of
this book.
The term PRIMITIVE is used here not in a pejorative sense, but
rather in the sense that the theory consisted of a collection of
analyses of specific processes by mathematical methods appropriate
to, and often invented to deal with, the specific process, rather
than an organized body of knowledge that characterizes the
classical and the modern period.
Although feedback principles can be recognized in the technology
of the Middle Ages and earlier, the intentional use of feedback
to improve the performance of dynamic systems was started at
around the beginning of the industrial revolution in the late
18th and early 19th centuries. The benchmark development was the
ball-governor invented by James Watt to control the speed of his
steam engine. Throughout the first half of the 19th century,
engineers and "mechanics" were inventing improved governors.
The theoretical principles that describe their operation were
studied by such luminaries of 18th and 19th century mathematical
physics as Huygens, Hooke, Airy, and Maxwell. By the mid 19th
century it was understood that the stability of a dynamic system
was determined by the location of the roots of the algebraic
equation. Rough in his Adams Prize Essay of 1877 invented the
stability algorithm that bears his name.
Mathematical problems that had arisen in the stability of
feedback control systems (as well as in other dynamic systems
including celestial mechanics) occupied the attention of early
20th century mathematicians Poincare and Liapunov, both of whom
made important contributions that have yet to be superseded.
Development of the gyroscope as a practical navigation instrument
during the first quarter of the 20th century led to the development
of a variety of autopilots for aircraft (and also for ships).
Theoretical problems of stabilizing these systems and improving
their performance engaged various mathematicians of the period.
Notable among them was N. Minorsky whose mimeographed notes on
nonlinear systems were virtually the only text on the subject
before 1950.
The CLASSICAL period of control theory begins during World War
II in the Radiation Laboratory of the Massachusetts Institute
of Technology. The personnel of the Radiation Laboratory included
a number of engineers, physicists, and mathematicians concerned
with solving engineering problems that arose in the war effort,
including radar and advanced fire control systems. The
laboratory that was assigned problems in control systems
included individuals knowledgeable in the frequency response
methods, developed by people such as Nyquist and Bode for
communication systems, as well as by engineers familiar with
other techniques. Working together, they evolved a systematic
control theory which is not tied to any particular application.
Use of frequency-domain (Laplace transform) methods made possible
the representation of a process by its transfer function and
thus permitted a visualization of the interaction of the various
subsystems in a complex system by the interconnection of the
transfer functions in the block diagram. The block diagram
contributed perhaps as much as any other factor to the development
of control theory as a distinct discipline. Now it was possible
to study the dynamic behavior of a hypothetical system by
manipulating and combining the black boxes in the block diagram
without having to know what goes on inside the boxes.
The classical period of control theory, characterized by
frequency-domain analysis, is still going strong, and is now
in a "neoclassical" phase -- with the development of various
sophisticated techniques for multivariable systems. But
concurrent with it is the MODERN period, which began in the
late 1950s and early 1960s.
STATE-SPACE METHODS are the cornerstone of MODERN CONTROL THEORY.
The essential feature of state-space methods is the characterization
of the processes of interest by differential equations instead of
transfer functions. This may seem like a throwback to the earlier,
primitive, period where differential equations also constituted the
means of representing the behavior of dynamic processes. But in the
earlier period the processes were simple enough to be characterized
by a SINGLE differential equation of fairly low order. In the
modern approach the processes are characterized by systems of
coupled, first-order differential equations. In principle there
is no limit to the order (i.e., the number of independent first-order
differential equations) and in practice the only limit to the order
is the availability of computer software capable of performing the
required calculations reliably.
Although the roots of modern control theory have their origins in
the early 20th century, in actuality they are intertwined with the
concurrent development of computers. A digital computer is all but
essential for performing the calculations that must be done in a
typical application.
There is more detail on this transition in "A Brief History of
Feedback Control" from "Optimal Control and Estimation" (1992)
by F. L. Lewis.
(
www.theorem.net/theorem/lewis1.html )
Of course the cheap computers in the 1980s also made possible
the breakthroughs of Stephen Wolfram, and the methodology he used
of doing extremely long-duration computer-simulated mathematical
experiments.
WARNING: OBJECTS IN MODEL MAY BE LESS PREDICTABLE THAN THEY APPEAR
Q: How many surrealists does it take to change a light bulb?
A: A fish.
-- joke
But let us always remember, a model is just a model;
the map may not match the territory. This is easy to pledge,
but when we get into the thick of things, it's harder to do.
I remember Bateson used to talk about 'diachronic' systems
which repeat themselves, and 'synchronic' systems which don't.
(I think the terms arose with anthropologists analyzing myths,
contrasting the non-repeating cultures such as Messianic Judaism and
Oceana's Cargo Cults, vs. the repeating cycle cultures like
the Mayans with their calendar and the Tibetans with their
prayer wheels.) In the middle of debating whether a certain system
"is" diachronic, Bateson would stop to remind us that these terms
apply only to MODELS OF REALITY. A certain MODEL is one or the other,
but not real reality.
This concept of "real reality" is a tough one. It's easy to
argue that it's just another model. One begins to appreciate
why Lao Tzu wrote:
The way that can be spoken is not the eternal way.
in the "Tao Te Ching" (4th Century BC).
(
www.amazon.com/exec/obidos/ASIN/014044131X/hip-20 )
When doing science, the thing to remember is the bug may
not be in the simulation or the data, it may be in the theory.
Remember what Isaac Asimov said:
The most exciting phrase to hear in science, the one that
heralds new discoveries, is not Eureka! (I found it!) but
rather, "hmm.... that's funny...."
DO IT YOURSELF
People only remember:
* 10% of what they read;
* 20% of what they hear;
* 30% of what they see;
* 50% of what they see and hear together;
* And 80% of what they see, hear, and do.
-- attributed to Dr. Mehrabians
(
www.getworldpassport.com/UK/marketplace.aspx?ID=MW )
There's no doubt. You have to do it yourself. Find a way
to play with simulations.
Some of Richardson's critics (and more recent critics of computer
modeling) said that you only get out of a computer a confirmation
of the assumptions that you put in. Oh that it were so! I have
found that to be a rare occurrence. More frequently I find that
my assumptions DO NOT lead to my conclusions, and I have to re-examine
them. Modeling is humbling, and it reminds me there are many
mysteries in those uncharted waters we call COMPLEXITY.
Here are some resources to help you find some sim software that
suits you.
Summary pages:
Individual packages (my favorites are in the section following this one):
PERSONAL FAVES
A program is like a nose;
Sometimes it runs, sometimes it blows.
-- Howard Rose
(quoted in "Computer Lib/Dream Machines" (book, 1974)
by Ted Nelson)
(
www.amazon.com/exec/obidos/ASIN/0893470023/hip-20 )
(
www.digibarn.com/collections/books/computer-lib )
There are a few programs I've played with myself, that I can highly
recommend:
- Stella
( www.iseesystems.com/softwares/Education/StellaSoftware.aspx )
very good for learning general systems theory
included in the book "Modeling Dynamic Systems: Lessons for a
First Course" by Diana Fisher
( www.iseesystems.com/store/modelingbook/default.aspx )
and in "Dynamic Modeling (Modeling Dynamic Systems)" by
D. H. Meadows
( www.amazon.com/exec/obidos/ASIN/0387988688/hip-20 )
- VisSim - Modeling and Simulation of Complex Dynamic Systems
( www.vissim.com )
( https://journal.fluid.power.net/issue2/software.html )
written by a fiend of mine, Peter Darnell, who left Stellar
to "do something with visual programming" and ended up
as CEO of Visual Solutions - read his amazing account
of controlling a prototype Antiskid Braking System (ABS)
with a laptop running VisSim
( www.adeptscience.co.uk/products/mathsim/vissim/apps/gm.html )
- Mathematica
( amath.colorado.edu/computing/Mathematica/basics/odes )
when I was first learning how to solve linear ODEs at
UCLA course taught by a satellite dynamics engineer,
and working at Stellar with my own graphics supercomputer
running mathematica, Craig Upson suggested I use the
graphics in Mathematica to visualize the ODEs behaviors
-- it was great advice
- AVS5
( www.avs.com )
I worked for this company for four years and used
its products for three years before that and for
ten years since; what can I say, I love this software
-- it's visually programmed visualization software, and
you can add module in C
I did some visualization of 2D and 3D ODEs with it, and posted
some of it on-line (also did some videos which I ought to
digitize)
( www.well.com/~abs/math_rec.html )
- NeatTools
( www.pulsar.org/neattools )
( www.pulsar.org/images/neatimages/index.html )
this free tool created by my friend Dave Warner's company
Mindtel is very handy for hooking up real time data for
low-cost Digital Signal Processing (DSP) prototyping --
you can add modules in C++
- write your own code
nothing beats REALLY doing it yourself
here's some (buggy) C code:
/* simulate linear n-dimensional system with Euler's method */
main() {
int t, v;
float state_array[NUMBER_OF_VARIABLES]
float transition_matrix[NUMBER_OF_VARIABLES][NUMBER_OF_VARIABLES];
void initialize_change_rules(transition_matrix);
void initialize_state(state_array);
void display(state_array);
float apply_change_rules(int v, state_array, transition_matrix);
for (t = 0; t < MAX_TIME STEPS; t++) {
for (v = 0; v < NUMBER_OF_VARIABLES; v++) {
state_array[v] =
state_array[v] +
apply_change_rules(v, state_array, transition_matrix);
display(state_array);
}
}
}
float apply_change_rules(int v, state_array, transition_matrix) {
int n;
float sum = 0;
for (n = 0; n < NUMBER_OF_VARIABLES; n++) {
sum = sum + transition_matrix[v][n]*state_array[n];
}
I leave it to the reader to write the routines:
initialize_change_rules(transition_matrix)
initialize_state(state_array)
display(state_array)
EXTRA CREDIT
The thing that got me started on the science that I've been
building now for about 20 years or so was the question of
okay, if mathematical equations can't make progress in
understanding complex phenomena in the natural world, how
might we make progress?
-- Stephen Wolfram
(
www.brainyquote.com/quotes/authors/s/stephen_wolfram.html )
While working on this article I got an email from Wolfram's crew
inviting me to the New Kind of Science (NKS) NKS summer school.
(
www.wolframscience.com/summerschool )
I was interested, but the course is three weeks long and I
don't have that much time off accrued. But it was fun to
imagine anyway. Skimming the email I noticed this passage:
The core of the Summer School is an individual project
done by each student. The project is chosen on the basis
of each student's interests, in discussion with Stephen
Wolfram and the Summer School instructors.
I thought to myself, "What would my project be?" And the answer
I came up with was "Simulate all possible systems." So I did.
First I worked out some simple cases by hand.

(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/system_sketch1.jpg )
Then I wrote a program in the C language (simple and portable) that
I called "all_systems" which I have posted in source code form
on my web site.
(
www.well.com/~abs/swdev/C/all_systems )
You might think that this is like trying to get a million monkeys
with typewriters to write Shakespeare (though I think James Joyce might
be easier) but in fact I learned quite a bit from the exercise.
First I looked at all possible deterministic finite systems --
so called "finite state machines" -- of a given size, having each
start in state 1. (By symmetry arguments I believed I didn't
have to check any of the other starting states to see all modes
of behavior.) Going in increasing order of size, here is what
I found. Systems having one state have only one behavior: the system
stays in state 1 with each time step. (I believe I could have solved
this analytically.) I call this an orbit with period 1. Systems having
two states can stay in one state (orbit of period 1), or oscillate between
two states (orbit of period 2), or start in one state, move to the other
and stay there (I call this a head of length 1 followed by an orbit of
period 1. Control engineers call it a transient followed by a stable mode.)
At this point we seen most of the behavioral modes. There is a head of
length L followed by an orbit of period P, and L + P <= N, the number
of states.
Here is how I would plot this, for example in a 3-state system:
+---+---+---+
| 2 | 3 | 1 |
+---+---+---+
| 1 | | |
| | 1 | |
| | | 1 |
| 1 | | |
+---+---+---+
Along the top row is the transition table (states are number left to
right): from 1 to 2, from 2 to 3 and from 3 to 1. Below are the steps,
starting in state 1, the system goes into state 2, then state 3, then
back to state 1. The head is length zero and the orbit is period three.
Looking at systems of three, four and five states I began adding some
automatic analysis to my program, that would count the times I had
heads an orbits of various lengths.
I wasn't able to get much bigger, because the number of different systems
with N states (before attempting to eliminate symmetries) is N^N -- a
function I mentioned in passing in C3M Volume 2 Number 9, Sep. 2003,
"Do Nothing, Oscillate, or Blow Up: An Exploration of the Laplace
Transform"
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/c3m_0209.txt )
although I had no idea at the time that it appears in systems theory.
Here's a table:
N N^N
- -------
1 1
2 4
3 27
4 256
5 3,125
6 46,656
7 823,543
Obviously it grows faster than e^N, so it is super-exponential.
I knew I couldn't go much higher, so I looked for something else to do.
I took the results of my analysis of head and orbit lengths:
head: 0 orbit: 0 count: 0 percent: 0.0
head: 1 orbit: 0 count: 0 percent: 0.0
head: 2 orbit: 0 count: 0 percent: 0.0
head: 3 orbit: 0 count: 0 percent: 0.0
head: 0 orbit: 1 count: 27 percent: 33.333333
head: 1 orbit: 1 count: 18 percent: 22.222222
head: 2 orbit: 1 count: 6 percent: 7.407407
head: 3 orbit: 1 count: 0 percent: 0.0
head: 0 orbit: 2 count: 18 percent: 22.222222
head: 1 orbit: 2 count: 6 percent: 7.407407
head: 2 orbit: 2 count: 0 percent: 0.0
head: 3 orbit: 2 count: 0 percent: 0.0
head: 0 orbit: 3 count: 6 percent: 7.407407
head: 1 orbit: 3 count: 0 percent: 0.0
head: 2 orbit: 3 count: 0 percent: 0.0
head: 3 orbit: 3 count: 0 percent: 0.0
loaded it into AVS and visualized a 2D array of data as bar charts.

(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/percents.jpg )
I showed it to some people. Nobody cared.
Then I got to thinking. This is such a simple model, maybe initial
condition is a more important part of it. Within the N^N different
systems at each size I decided to look at how the choice of initial
condition influenced system behavior. Now I was looking for families
of trajectories, N of them, making the total "runs" I had to compute
grow to N*N^N, or N^(N+1). But maybe eliminating these combinations
before with "symmetry" arguments had been a bad move.
I had to find a way to plot the families of of trajectories.
This is what I came up with (shown for a six state system):
+--------+--------+--------+--------+--------+--------+
| 2 | 2 | 1 | 1 | 1 | 1 |
+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 3 | 4 | 5 | 6 |
| 3456 | 12 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
+--------+--------+--------+--------+--------+--------+
Actually, I drew this representation by hand for the N=3 case
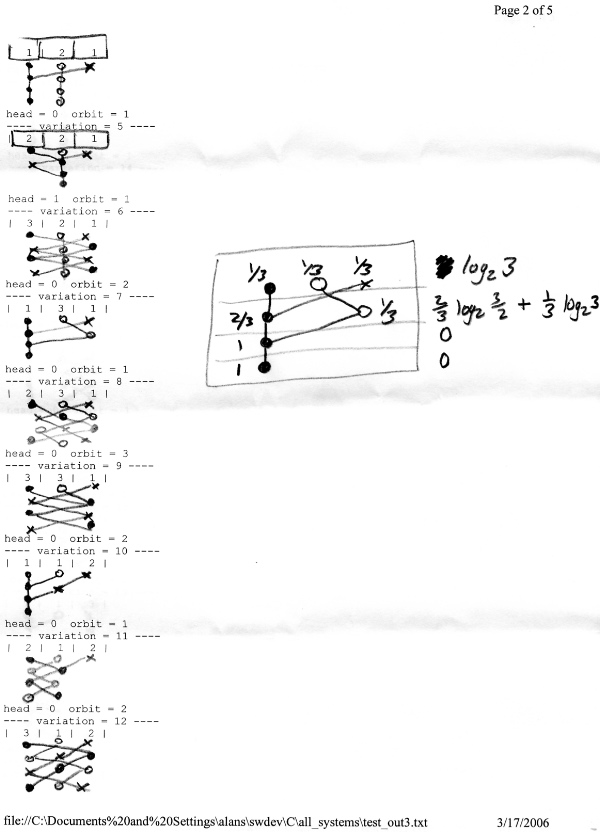
(
www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/system_sketch2.jpg )
before I wrote the code. (The calculations on the side are computing
the entropy loss -- i.e. information gained -- if you learn the state
at each step, assuming equal distribution of start probablities.)
From these three experiences of doing it by hand, writing a program
to do it, and then looking at the output, I learned more: one of
these systems is always doing one of two things: either destroying
information, or preserving it. This corresponds to entropy increasing
or staying the same. In the above 6-dim example, from step 1 to 2
an initial condition of 1 or 2 both jump to state 2, destroying the
information of which state you came from. In the next step trajectories
from 3 through 6 join in, destroying more information. After that
the system preserves the remaining information that it is in state 2.
I also realized that being in orbit of period greater than one means
a system also has "phase information."
Consider this 6-state system, looking only at the initial states
of 1 & 6:
+--------+--------+--------+--------+--------+--------+
| 6 | 6 | 3 | 1 | 1 | 1 |
+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 3 | 4 | 5 | 6 |
| 456 | | 3 | | | 12 |
| 12 | | 3 | | | 456 |
| 456 | | 3 | | | 12 |
| 12 | | 3 | | | 456 |
| 456 | | 3 | | | 12 |
+--------+--------+--------+--------+--------+--------+
One goes to six and six goes to one. But depending on where
you start there are two orbits that crisscross like shoe
laces. This system can store a "bit" of information in just
where it is at a given time in this orbit. (The longer the
orbit period the more information can be stored.)
This is what I've discovered in a few days' time. (Okay,
I'll grant it must be a rediscovery, but I've VERY THOROUGHLY
learned this by doing it myself.)
I wonder YOU can discover?
POSTSCRIPT
Though you all would want to know about "Sonoma 2006: The 50th Annual
Meeting of the International Society for the Systems Sciences"
(
www.isss.org/conferences/sonoma2006 )
being held at Sonoma State University, Rohnert Park, California, USA
July 9th - 14th 2006. From the web site:
The 50th anniversary conference of the International Society for
the Systems Sciences offers an opportunity to celebrate a half-century
of theory and practice in the broadly defined field of systems,
honoring the vision of the founders (Ludwig von Bertalanffy,
Kenneth Boulding, Ralph Gerard, James Grier Miller, and Anatol
Rapoport) and recognizing the contributions of leading systems
thinkers. It is also a time to reflect upon what we have learned,
and to collaboratively envision future directions.
* * * * *
Pre-Conference Workshop: Mind in Nature: Gregory Bateson and the
Ecology of Experience, July 7 - 9
Errata
Last time's issue was emailed out with a header that said "Volume 4
Number 8, Nov. 2005" by mistake instead of the correct "Volume 5
Number 1, Jan. 2006." Also, I misspelled the names Lasseter and
Catmull (as Lassiter and Catmul, my spell-checker didn't catch them);
both these errors have been corrected in the archives.
========================================================================
newsletter archives:
www.well.com/~abs/Cyb/4.669211660910299067185320382047
========================================================================
Privacy Promise: Your email address will never be sold or given to
others. You will receive only the e-Zine C3M from me, Alan Scrivener,
at most once per month. It may contain commercial offers from me.
To cancel the e-Zine send the subject line "unsubscribe" to me.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I receive a commission on everything you purchase from Amazon.com after
following one of my links, which helps to support my research.
========================================================================
Copyright 2006 by Alan B. Scrivener
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/time-life_topology.jpg )
but I didn't know it was INVENTED to solve problems in systems theory.
Elsewhere in the book was a turgid discussion of the unsolved "three
body problem," which I had no clue was connected to topology.
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/time-life_topology.jpg )
but I didn't know it was INVENTED to solve problems in systems theory.
Elsewhere in the book was a turgid discussion of the unsolved "three
body problem," which I had no clue was connected to topology.
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/time-life_3body.jpg )
After winning the King Oscar prize Poincare ruminated over what he had
learned by all this, and eventually published his conclusions in
"Science and Method" (1914).
( www.amazon.com/exec/obidos/ASIN/0486432696/hip-20 )
A more thorough academic study of this event and its consequences
appeared just a decade ago, in "Poincare and the Three-Body Problem
(History of Mathematics, V. 11)" ( book, 1996 ) by June Barrow-Green.
( www.amazon.com/exec/obidos/ASIN/0821803670/hip-20 )
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/time-life_3body.jpg )
After winning the King Oscar prize Poincare ruminated over what he had
learned by all this, and eventually published his conclusions in
"Science and Method" (1914).
( www.amazon.com/exec/obidos/ASIN/0486432696/hip-20 )
A more thorough academic study of this event and its consequences
appeared just a decade ago, in "Poincare and the Three-Body Problem
(History of Mathematics, V. 11)" ( book, 1996 ) by June Barrow-Green.
( www.amazon.com/exec/obidos/ASIN/0821803670/hip-20 )
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/margalef.jpg )
Both authors, Von Bertalanffy and Margalef, end up concluding that
systems must be studied, even if the tools are inadequate, and both
go on to advocate that HEURISTICS be used as stop-gap measures, such
as simplifications, analogies, intuition, etc., nibbling on the
corners of problems that can't be solved outright.
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/margalef.jpg )
Both authors, Von Bertalanffy and Margalef, end up concluding that
systems must be studied, even if the tools are inadequate, and both
go on to advocate that HEURISTICS be used as stop-gap measures, such
as simplifications, analogies, intuition, etc., nibbling on the
corners of problems that can't be solved outright.
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/scientific.jpg )
And they would have probably gone on indefinitely building better bombs
this way except that some funky things kept happening, like turbulence.
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/scientific.jpg )
And they would have probably gone on indefinitely building better bombs
this way except that some funky things kept happening, like turbulence.
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/richardson.jpg )
But as the Eames explained:
Richardson was a Quaker and conscientious objector. His wife
recalled, "There came a time of heartbreak when those most
interested in his 'upper air' researches proved to be the
'poison gas' experts. Lewis stopped his meteorology researches,
destroying such as had not been published. What this cost him
none will ever know!"
He devoted the rest of his life to the mathematical study of the
causes of war, publishing several books on the subject and single-
handedly founding quantitative sociology. His "Arms and Insecurity"
(written in 1953 -- the year of his death -- and published in 1960)
( www.amazon.com/exec/obidos/ASIN/0835703789/hip-20 )
presents a model of an arms race between two nations. Let's map
it on to the checkerboard game. Say that the lower left corner
(square 1) represents each nation spending nothing on arms.
Then motion to the right represents nation A spending more on arms,
in increments of 2% of its Gross National Product (GNP), while
moving up represents nation B spending more on arms. Let's assume
the nations behave in a perfectly symmetrical manner. Each time
step will be a year, a typical government funding cycle.
Now you have to ask yourself, if you were Minister of Finance for
nation A, and you were spending 6% of your GNP on arms while your
hostile neighbor nation B spent 10% of their GNP, what would
do next year? Then you have to do it again for every combination
of A and B's spending on the board.
It quickly become obvious that for "reasonable" human responses to
each scenario you end up with a system in which the state moves
up and to the right, in an unending arms race (at least until you
run out of checkerboard. I think the U.S. and its allies won the
Cold War and beat the U.S.S.R. because they ran out of checkerboard
first.) But up until that time things were pretty dicey. Richardson
quoted Sir Edward Grey, British Foreign Secretary a the start of
World War I:
The increase of armaments that is intended in each nation
to produce consciousness of strength, and a sense of security,
does not produce these effects.
Our little checkerboard model helps us understand why.
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/richardson.jpg )
But as the Eames explained:
Richardson was a Quaker and conscientious objector. His wife
recalled, "There came a time of heartbreak when those most
interested in his 'upper air' researches proved to be the
'poison gas' experts. Lewis stopped his meteorology researches,
destroying such as had not been published. What this cost him
none will ever know!"
He devoted the rest of his life to the mathematical study of the
causes of war, publishing several books on the subject and single-
handedly founding quantitative sociology. His "Arms and Insecurity"
(written in 1953 -- the year of his death -- and published in 1960)
( www.amazon.com/exec/obidos/ASIN/0835703789/hip-20 )
presents a model of an arms race between two nations. Let's map
it on to the checkerboard game. Say that the lower left corner
(square 1) represents each nation spending nothing on arms.
Then motion to the right represents nation A spending more on arms,
in increments of 2% of its Gross National Product (GNP), while
moving up represents nation B spending more on arms. Let's assume
the nations behave in a perfectly symmetrical manner. Each time
step will be a year, a typical government funding cycle.
Now you have to ask yourself, if you were Minister of Finance for
nation A, and you were spending 6% of your GNP on arms while your
hostile neighbor nation B spent 10% of their GNP, what would
do next year? Then you have to do it again for every combination
of A and B's spending on the board.
It quickly become obvious that for "reasonable" human responses to
each scenario you end up with a system in which the state moves
up and to the right, in an unending arms race (at least until you
run out of checkerboard. I think the U.S. and its allies won the
Cold War and beat the U.S.S.R. because they ran out of checkerboard
first.) But up until that time things were pretty dicey. Richardson
quoted Sir Edward Grey, British Foreign Secretary a the start of
World War I:
The increase of armaments that is intended in each nation
to produce consciousness of strength, and a sense of security,
does not produce these effects.
Our little checkerboard model helps us understand why.
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/SG2002/sickscan.jpg )
But the two best methods I have happened upon for visualizing higher
dimensions I call the "N-Dimensional Tic Tac Toe" and "N-Dimensional
Elevator" metaphors.
In "N-Dimensional Tic Tac Toe" I like to play 4-in-a-row because otherwise
the center square is a super-duper square, and the first player has a
huge advantage. You know how to draw a 2D game. To make a 3D game just
draw 4 2D games in a row, separated by a little space. Those are the
4 slices in the third dimension, like the floor plan to a low-rise building.
Then duplicate this 4-in-a-row pattern of 2D game fields three more times
below, making a 2D array of 2D arrays. There's your 4D game. This will
easily fit on an 8.5x11 inch sheet of paper, and you can draw it and
photocopy it to make playing fields for real 4D tick-tack-toe games.
Great for older kids on car trips. A win is (1,1,1,1),(1,1,1,2),(1,1,1,3),
(1,1,1,4) for example, or (1,4,4,1),(2,3,3,1),(3,2,2,1),(4,1,1,1).
Each independent coordinate has to stay the same or rise/fall by a unit
with each X or O position to form 4 in a 4D row.
Now, you can make a row of 4 of these pages, and get a 5D game,
or make a 4x4 array of them on the floor, and get a 6D game, and so
on. You may need some sheets of poster board for the next steps.
The other metaphor is the "N-Dimensional Elevator" which is much simpler.
Let's say you're in a 13-story 7-dimensional building full of large,
windowless apartments. Each apartment is only 3D, so you'll feel at
home, and the elevator is 3D so humans can ride in it, but you get in
and there are 7 vertical columns of buttons, one for each dimension,
and each column has 13 buttons for the 13 "floors" in that dimension.
Like a Chinese menu, you select one from each column, and then the
elevator takes you there. Anything you leave in an apartment you will
find there later by pushing the same buttons. But if you leave a barking
dog the neighbors in 14 directions (instead of 6 directions in a 3D
building) might complain.
After much thought I have concluded that if a Turing Machine can simulate
a system of any dimensionality (and it can, and so can any computer)
then dimensions don't matter so much in finite systems. The checkerboard
model I described previously sometimes acted 2D and sometimes 1D, but
because in the most general case any state could lead to any other, you
COULD argue that it's an INFINITE-dimensional system. Only by REMOVING
transitions can you constrain it to act 2D, as in the model of the
Richardson arms race.
Something else I've been pondering is this: if we found chaos by going
from 2D to 3D, what is waiting for us to discover in going from 101
dimensions to 102? (Not to mention all the steps along the way.)
I fear that these are the sorts of questions that only Wolfram's method
can answer: simulate all possibilities and look at the results.
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/SG2002/sickscan.jpg )
But the two best methods I have happened upon for visualizing higher
dimensions I call the "N-Dimensional Tic Tac Toe" and "N-Dimensional
Elevator" metaphors.
In "N-Dimensional Tic Tac Toe" I like to play 4-in-a-row because otherwise
the center square is a super-duper square, and the first player has a
huge advantage. You know how to draw a 2D game. To make a 3D game just
draw 4 2D games in a row, separated by a little space. Those are the
4 slices in the third dimension, like the floor plan to a low-rise building.
Then duplicate this 4-in-a-row pattern of 2D game fields three more times
below, making a 2D array of 2D arrays. There's your 4D game. This will
easily fit on an 8.5x11 inch sheet of paper, and you can draw it and
photocopy it to make playing fields for real 4D tick-tack-toe games.
Great for older kids on car trips. A win is (1,1,1,1),(1,1,1,2),(1,1,1,3),
(1,1,1,4) for example, or (1,4,4,1),(2,3,3,1),(3,2,2,1),(4,1,1,1).
Each independent coordinate has to stay the same or rise/fall by a unit
with each X or O position to form 4 in a 4D row.
Now, you can make a row of 4 of these pages, and get a 5D game,
or make a 4x4 array of them on the floor, and get a 6D game, and so
on. You may need some sheets of poster board for the next steps.
The other metaphor is the "N-Dimensional Elevator" which is much simpler.
Let's say you're in a 13-story 7-dimensional building full of large,
windowless apartments. Each apartment is only 3D, so you'll feel at
home, and the elevator is 3D so humans can ride in it, but you get in
and there are 7 vertical columns of buttons, one for each dimension,
and each column has 13 buttons for the 13 "floors" in that dimension.
Like a Chinese menu, you select one from each column, and then the
elevator takes you there. Anything you leave in an apartment you will
find there later by pushing the same buttons. But if you leave a barking
dog the neighbors in 14 directions (instead of 6 directions in a 3D
building) might complain.
After much thought I have concluded that if a Turing Machine can simulate
a system of any dimensionality (and it can, and so can any computer)
then dimensions don't matter so much in finite systems. The checkerboard
model I described previously sometimes acted 2D and sometimes 1D, but
because in the most general case any state could lead to any other, you
COULD argue that it's an INFINITE-dimensional system. Only by REMOVING
transitions can you constrain it to act 2D, as in the model of the
Richardson arms race.
Something else I've been pondering is this: if we found chaos by going
from 2D to 3D, what is waiting for us to discover in going from 101
dimensions to 102? (Not to mention all the steps along the way.)
I fear that these are the sorts of questions that only Wolfram's method
can answer: simulate all possibilities and look at the results.
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/system_sketch1.jpg )
Then I wrote a program in the C language (simple and portable) that
I called "all_systems" which I have posted in source code form
on my web site.
( www.well.com/~abs/swdev/C/all_systems )
You might think that this is like trying to get a million monkeys
with typewriters to write Shakespeare (though I think James Joyce might
be easier) but in fact I learned quite a bit from the exercise.
First I looked at all possible deterministic finite systems --
so called "finite state machines" -- of a given size, having each
start in state 1. (By symmetry arguments I believed I didn't
have to check any of the other starting states to see all modes
of behavior.) Going in increasing order of size, here is what
I found. Systems having one state have only one behavior: the system
stays in state 1 with each time step. (I believe I could have solved
this analytically.) I call this an orbit with period 1. Systems having
two states can stay in one state (orbit of period 1), or oscillate between
two states (orbit of period 2), or start in one state, move to the other
and stay there (I call this a head of length 1 followed by an orbit of
period 1. Control engineers call it a transient followed by a stable mode.)
At this point we seen most of the behavioral modes. There is a head of
length L followed by an orbit of period P, and L + P <= N, the number
of states.
Here is how I would plot this, for example in a 3-state system:
+---+---+---+
| 2 | 3 | 1 |
+---+---+---+
| 1 | | |
| | 1 | |
| | | 1 |
| 1 | | |
+---+---+---+
Along the top row is the transition table (states are number left to
right): from 1 to 2, from 2 to 3 and from 3 to 1. Below are the steps,
starting in state 1, the system goes into state 2, then state 3, then
back to state 1. The head is length zero and the orbit is period three.
Looking at systems of three, four and five states I began adding some
automatic analysis to my program, that would count the times I had
heads an orbits of various lengths.
I wasn't able to get much bigger, because the number of different systems
with N states (before attempting to eliminate symmetries) is N^N -- a
function I mentioned in passing in C3M Volume 2 Number 9, Sep. 2003,
"Do Nothing, Oscillate, or Blow Up: An Exploration of the Laplace
Transform"
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/c3m_0209.txt )
although I had no idea at the time that it appears in systems theory.
Here's a table:
N N^N
- -------
1 1
2 4
3 27
4 256
5 3,125
6 46,656
7 823,543
Obviously it grows faster than e^N, so it is super-exponential.
I knew I couldn't go much higher, so I looked for something else to do.
I took the results of my analysis of head and orbit lengths:
head: 0 orbit: 0 count: 0 percent: 0.0
head: 1 orbit: 0 count: 0 percent: 0.0
head: 2 orbit: 0 count: 0 percent: 0.0
head: 3 orbit: 0 count: 0 percent: 0.0
head: 0 orbit: 1 count: 27 percent: 33.333333
head: 1 orbit: 1 count: 18 percent: 22.222222
head: 2 orbit: 1 count: 6 percent: 7.407407
head: 3 orbit: 1 count: 0 percent: 0.0
head: 0 orbit: 2 count: 18 percent: 22.222222
head: 1 orbit: 2 count: 6 percent: 7.407407
head: 2 orbit: 2 count: 0 percent: 0.0
head: 3 orbit: 2 count: 0 percent: 0.0
head: 0 orbit: 3 count: 6 percent: 7.407407
head: 1 orbit: 3 count: 0 percent: 0.0
head: 2 orbit: 3 count: 0 percent: 0.0
head: 3 orbit: 3 count: 0 percent: 0.0
loaded it into AVS and visualized a 2D array of data as bar charts.
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/system_sketch1.jpg )
Then I wrote a program in the C language (simple and portable) that
I called "all_systems" which I have posted in source code form
on my web site.
( www.well.com/~abs/swdev/C/all_systems )
You might think that this is like trying to get a million monkeys
with typewriters to write Shakespeare (though I think James Joyce might
be easier) but in fact I learned quite a bit from the exercise.
First I looked at all possible deterministic finite systems --
so called "finite state machines" -- of a given size, having each
start in state 1. (By symmetry arguments I believed I didn't
have to check any of the other starting states to see all modes
of behavior.) Going in increasing order of size, here is what
I found. Systems having one state have only one behavior: the system
stays in state 1 with each time step. (I believe I could have solved
this analytically.) I call this an orbit with period 1. Systems having
two states can stay in one state (orbit of period 1), or oscillate between
two states (orbit of period 2), or start in one state, move to the other
and stay there (I call this a head of length 1 followed by an orbit of
period 1. Control engineers call it a transient followed by a stable mode.)
At this point we seen most of the behavioral modes. There is a head of
length L followed by an orbit of period P, and L + P <= N, the number
of states.
Here is how I would plot this, for example in a 3-state system:
+---+---+---+
| 2 | 3 | 1 |
+---+---+---+
| 1 | | |
| | 1 | |
| | | 1 |
| 1 | | |
+---+---+---+
Along the top row is the transition table (states are number left to
right): from 1 to 2, from 2 to 3 and from 3 to 1. Below are the steps,
starting in state 1, the system goes into state 2, then state 3, then
back to state 1. The head is length zero and the orbit is period three.
Looking at systems of three, four and five states I began adding some
automatic analysis to my program, that would count the times I had
heads an orbits of various lengths.
I wasn't able to get much bigger, because the number of different systems
with N states (before attempting to eliminate symmetries) is N^N -- a
function I mentioned in passing in C3M Volume 2 Number 9, Sep. 2003,
"Do Nothing, Oscillate, or Blow Up: An Exploration of the Laplace
Transform"
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/c3m_0209.txt )
although I had no idea at the time that it appears in systems theory.
Here's a table:
N N^N
- -------
1 1
2 4
3 27
4 256
5 3,125
6 46,656
7 823,543
Obviously it grows faster than e^N, so it is super-exponential.
I knew I couldn't go much higher, so I looked for something else to do.
I took the results of my analysis of head and orbit lengths:
head: 0 orbit: 0 count: 0 percent: 0.0
head: 1 orbit: 0 count: 0 percent: 0.0
head: 2 orbit: 0 count: 0 percent: 0.0
head: 3 orbit: 0 count: 0 percent: 0.0
head: 0 orbit: 1 count: 27 percent: 33.333333
head: 1 orbit: 1 count: 18 percent: 22.222222
head: 2 orbit: 1 count: 6 percent: 7.407407
head: 3 orbit: 1 count: 0 percent: 0.0
head: 0 orbit: 2 count: 18 percent: 22.222222
head: 1 orbit: 2 count: 6 percent: 7.407407
head: 2 orbit: 2 count: 0 percent: 0.0
head: 3 orbit: 2 count: 0 percent: 0.0
head: 0 orbit: 3 count: 6 percent: 7.407407
head: 1 orbit: 3 count: 0 percent: 0.0
head: 2 orbit: 3 count: 0 percent: 0.0
head: 3 orbit: 3 count: 0 percent: 0.0
loaded it into AVS and visualized a 2D array of data as bar charts.
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/percents.jpg )
I showed it to some people. Nobody cared.
Then I got to thinking. This is such a simple model, maybe initial
condition is a more important part of it. Within the N^N different
systems at each size I decided to look at how the choice of initial
condition influenced system behavior. Now I was looking for families
of trajectories, N of them, making the total "runs" I had to compute
grow to N*N^N, or N^(N+1). But maybe eliminating these combinations
before with "symmetry" arguments had been a bad move.
I had to find a way to plot the families of of trajectories.
This is what I came up with (shown for a six state system):
+--------+--------+--------+--------+--------+--------+
| 2 | 2 | 1 | 1 | 1 | 1 |
+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 3 | 4 | 5 | 6 |
| 3456 | 12 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
+--------+--------+--------+--------+--------+--------+
Actually, I drew this representation by hand for the N=3 case
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/percents.jpg )
I showed it to some people. Nobody cared.
Then I got to thinking. This is such a simple model, maybe initial
condition is a more important part of it. Within the N^N different
systems at each size I decided to look at how the choice of initial
condition influenced system behavior. Now I was looking for families
of trajectories, N of them, making the total "runs" I had to compute
grow to N*N^N, or N^(N+1). But maybe eliminating these combinations
before with "symmetry" arguments had been a bad move.
I had to find a way to plot the families of of trajectories.
This is what I came up with (shown for a six state system):
+--------+--------+--------+--------+--------+--------+
| 2 | 2 | 1 | 1 | 1 | 1 |
+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 3 | 4 | 5 | 6 |
| 3456 | 12 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
| | 123456 | | | | |
+--------+--------+--------+--------+--------+--------+
Actually, I drew this representation by hand for the N=3 case
 ( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/system_sketch2.jpg )
before I wrote the code. (The calculations on the side are computing
the entropy loss -- i.e. information gained -- if you learn the state
at each step, assuming equal distribution of start probablities.)
From these three experiences of doing it by hand, writing a program
to do it, and then looking at the output, I learned more: one of
these systems is always doing one of two things: either destroying
information, or preserving it. This corresponds to entropy increasing
or staying the same. In the above 6-dim example, from step 1 to 2
an initial condition of 1 or 2 both jump to state 2, destroying the
information of which state you came from. In the next step trajectories
from 3 through 6 join in, destroying more information. After that
the system preserves the remaining information that it is in state 2.
I also realized that being in orbit of period greater than one means
a system also has "phase information."
Consider this 6-state system, looking only at the initial states
of 1 & 6:
+--------+--------+--------+--------+--------+--------+
| 6 | 6 | 3 | 1 | 1 | 1 |
+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 3 | 4 | 5 | 6 |
| 456 | | 3 | | | 12 |
| 12 | | 3 | | | 456 |
| 456 | | 3 | | | 12 |
| 12 | | 3 | | | 456 |
| 456 | | 3 | | | 12 |
+--------+--------+--------+--------+--------+--------+
One goes to six and six goes to one. But depending on where
you start there are two orbits that crisscross like shoe
laces. This system can store a "bit" of information in just
where it is at a given time in this orbit. (The longer the
orbit period the more information can be stored.)
This is what I've discovered in a few days' time. (Okay,
I'll grant it must be a rediscovery, but I've VERY THOROUGHLY
learned this by doing it myself.)
I wonder YOU can discover?
( www.well.com/~abs/Cyb/4.669211660910299067185320382047/Sim/system_sketch2.jpg )
before I wrote the code. (The calculations on the side are computing
the entropy loss -- i.e. information gained -- if you learn the state
at each step, assuming equal distribution of start probablities.)
From these three experiences of doing it by hand, writing a program
to do it, and then looking at the output, I learned more: one of
these systems is always doing one of two things: either destroying
information, or preserving it. This corresponds to entropy increasing
or staying the same. In the above 6-dim example, from step 1 to 2
an initial condition of 1 or 2 both jump to state 2, destroying the
information of which state you came from. In the next step trajectories
from 3 through 6 join in, destroying more information. After that
the system preserves the remaining information that it is in state 2.
I also realized that being in orbit of period greater than one means
a system also has "phase information."
Consider this 6-state system, looking only at the initial states
of 1 & 6:
+--------+--------+--------+--------+--------+--------+
| 6 | 6 | 3 | 1 | 1 | 1 |
+--------+--------+--------+--------+--------+--------+
| 1 | 2 | 3 | 4 | 5 | 6 |
| 456 | | 3 | | | 12 |
| 12 | | 3 | | | 456 |
| 456 | | 3 | | | 12 |
| 12 | | 3 | | | 456 |
| 456 | | 3 | | | 12 |
+--------+--------+--------+--------+--------+--------+
One goes to six and six goes to one. But depending on where
you start there are two orbits that crisscross like shoe
laces. This system can store a "bit" of information in just
where it is at a given time in this orbit. (The longer the
orbit period the more information can be stored.)
This is what I've discovered in a few days' time. (Okay,
I'll grant it must be a rediscovery, but I've VERY THOROUGHLY
learned this by doing it myself.)
I wonder YOU can discover?