========================================================================
Cybernetics in the 3rd Millennium (C3M) Volume 10 Number 2, July 2012
 Alan B. Scrivener — www.well.com/user/abs — mailto:abs@well.com
========================================================================

 

Alan Turing statue photo from www.mathcomp.leeds.ac.uk/turing2012



In this issue:


Short Subjects: WELL Warning;
"Systems Science" Facebook Group;
Belated Nora Bateson Events; Reading List



WELL Warning

Dear readers, I have had an account at The WELL since 1989.

    ( en.wikipedia.org/wiki/The_WELL )

I do get a lot of spam, but I like having a stable home on the internet.
But not anymore.  Current owner Slate has announced that the staff has
been laid off, no new subscribers are being accepted, and the domain is
for sale, with or without the community.  (This despite the world's
oldest on-line community being mildly profitable.)  So, at any time,
without notice, my primary email and web presence could vanish.  I haven't
decided where I will land yet (any suggestions?), so if this should happen,
Google me.  Thank you for your flexibility in this difficult time.

"Systems Science" Facebook Group

For up-to-the-minute news on systems sciences, I recommend the "Systems
Sciences" group on Facebook.

    ( www.facebook.com/groups/2391509563 )

Folks there have been live-blogging with their smart phones and tablets from
a few interesting looking systems-related conferences this summer, including
the  International Society for the Systems Sciences (ISSS) 2012 conference at
San Jose State University, California July 15 through 20,

    ( isss.org/world/sanjose-2012 )

and I've enjoyed tuning in.


Belated Nora Bateson Events

It looks like my timing didn't work out for this, but if I'd gotten this
'zine out 2 months ago like I once planned I could have alerted you to two
events involving Nora Bateson:

    

  •  Weekend of June 29-July 1, 2012
"An Ecology of Relationships in Life, Science and Art"
Esalen Institute, Big Sur, CA
Nora Bateson  &  Rex Weyler
webapp.esalen.org/workshops/11404


  •  Week of July 9-13, 2012
"2012 Joint Conference of The American Society for Cybernetics (ASC)
and Bateson Idea Group (BIG)"
Asilomar, CA
asc-cybernetics.org/2012


But I can't see any harm in listing these things belatedly, and perhaps
some good will come of it.

(Note that if you were in the above-mentioned "Systems Science"
Facebook group you would've gotten timely updates about these events.)

Also check out her latest interview on YouTube:

    www.youtube.com/watch?v=x8VFETiwQq4&fb_source=message

Nora Bateson interview by Scott Turner at State University of New York
College of Environmental Science and Forestry (SUNY-ESF).

More links:


Reading List


"Never read more than one book."

    — Gregory Bateson, 1974
        spoken to me after I told him I was reading several books at once,
        and then typed by his secretary Judith and posted on the office door


Much to my dismay I find I haven't actually finished any books in the last
four months, including the three I review below.  [Editor's note: now it's
been 6 months and I did finish a few.]  Just for giggles, then, I've listed
all the books on my "To Read" shelf that currently [May 2012] have a bookmark
in them:

    

  1.  Twain, Mark Roughing It (1872)
 [p. 74 of 422; 17%]
    ( www.amazon.com/exec/obidos/ASIN/1144838002/hip-20 )


  2.  Joyce, James Ulysses (novel, 1934)
 [p. 296 of 783; 37%]
    ( www.amazon.com/exec/obidos/ASIN/1613821174/hip-20 )


  3.  Hesse, Hermann The Glass Bead Game (Magister Ludi)  (novel, 1943)
 [p. 320 of 558; 57% — since about 1996]
    ( www.amazon.com/exec/obidos/ASIN/0312278497/hip-20 )


  4.  Roth, Ed "Big Daddy" Whatever Happened To the Beatnik Bandit? —
 Plus Photos of All Big Daddy Roth Cars — Compiled and Edited by Ed "Big Daddy" Roth (1964)
 [p. 9 of 40; 22%]
    ( www.worthpoint.com/worthopedia/ed-big-daddy-roth-whatever-happened-142832244 )


  5.  Cambell, Joseph Myths To Live By (1972)
 [p. 112 of 275; 40%]
    ( www.amazon.com/exec/obidos/ASIN/0285647318/hip-20 )


  6.  Bretnor, Reginald [ed.] The Craft of Science Fiction (1976)
 [p. 5 of 310; 1%]
    ( www.amazon.com/exec/obidos/ASIN/0064634574/hip-20 )


  7.  Tuchman, Barbara W. A Distant Mirror (1978)
 [p. 238 of 587; 40%]
    ( www.amazon.com/exec/obidos/ASIN/0345349571/hip-20 )


  8.  Heims, Steve J. The Cybernetics Group (1991)
 [p. 112 of 284; 39%]
    ( www.amazon.com/exec/obidos/ASIN/0262082004/hip-20 )


  9.  Silver, Alain & Ursini, James [eds.] Film Noir Reader (1996)
 [p. 136 of 339; 40%]
    ( www.amazon.com/exec/obidos/ASIN/0879101970/hip-20 )


  10.  Gilbert, Daniel Stumbling On Happiness (2006)
 [p. 34 of 263; 12%]
    ( www.amazon.com/exec/obidos/ASIN/1400077427/hip-20 )


  11.  Collins, Suzanne The Hunger Games (novel, 2008)
 [p. 55 of 374; 14%]
    ( www.amazon.com/exec/obidos/ASIN/0439023521/hip-20 )


  12.  Coupland, Douglas Generation A (novel, 2009)
 [p. 20 of 297; 6%]
    ( www.amazon.com/exec/obidos/ASIN/1439157014/hip-20 )


  13.  Shepard, Aaron POD [Print On Demand] for Profit: More on the
NEW Business of Self Publishing, or How to Publish Your Books With
Online Book Marketing and Print on Demand by Lightning Source (2010)
 [p. 226 of 271; 83%]
    ( www.amazon.com/exec/obidos/ASIN/0938497464/hip-20 )


  14.  Girardet, Edward Killing the Cranes: A Reporter's Journey Through Three Decades of War in Afghanistan (2011)
 [p. 13 of 397; 3%]
    ( www.amazon.com/exec/obidos/ASIN/1603583424/hip-20 )


  15.  Kinsey, Leonard The Dark Side of Disney (2011)
 [0%]
    ( www.amazon.com/exec/obidos/ASIN/0615506135/hip-20 )


  16.  Mamet, David The Secret Knowledge: On the Dismantling of American Culture (2011)
 [p. 80 of 726; 11%]
    ( www.amazon.com/exec/obidos/ASIN/1595230769/hip-20 )



Excursions in Graph Theory


a typical drawing of a graph, from "What is a Graph?" by Dale Winter
www.math.lsa.umich.edu/mmss/coursesONLINE/graph/graph1


"If you give me a list of your [Facebook] friends, that's just a list
of integers to me; there's not much I can do with it.  But if you give
me the social network, then I can really do some things..."

    — Max Nanis, social media & artificial intelligence programming expert
        presentation to San Diego Chapter of ACM SIGGRAPH
        "I'm Not a Real Friend, but I Play One on the Internet"
        15 February 2012


            ( san-diego.siggraph.org/pastevents.html )

I have written before in this 'zine about Graph Theory, also known as Network
Theory.  See C3M v. 3 n. 5: "Six Degrees of Buddy Hackett"

    ( www.well.com/user/abs/Cyb/archive/c3m_0305.html )

and also the note at the end of C3M v. 3 n. 6

    ( www.well.com/user/abs/Cyb/archive/c3m_0306.html )

I previously recommended some popular books on the subject:

and would like to add:



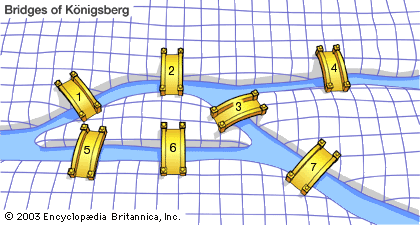a nice schematic of the seven bridges problem

                            * * * * * *

Graph Theory began with Euler's solving of the "Seven Bridges of Königsberg" problem in 1736.

    ( en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg )

Since then it has been useful in mathematics in the solution of puzzles,
and in the analysis of error-correcting codes, combinatorial problems, map
coloring problems and a host of other obscure topics; in addition it has
proved relevant in the "real world" in dealing with vehicle traffic, circuit
design, network routing, the patterns of leaking liquid nuclear waste
percolating through ground rock, and the dynamics of communications such
as rumors and fads, and disease epidemics.

But I realized last February, when I went to the local SIGGRAPH talk I quoted
above, that we'd reached a "tipping point" in the commerce world.  Companies
have been told that they need a "social media strategy" now for a few years,
and quite a few of them have gotten on board.  By now they must have
accumulated many terrabytes of data about the "social graphs" of their
customers, and now they're most certainly asking their "business analytics"
folks to analyze this data for marketing trends.  The giant internet companies
like Google, Facebook, Twitter, Amazon and Apple certainly must have their own
well-staffed departments doing social media research that will probably never
see the light of day.  Smaller companies are out shopping for similar
expertise.

Then I happened on a book I'd forgotten I owned:

I realized that I'd never actually read it, just used it as a reference.
I began working my way through it, and found it quite addictive.
One of the charming things about Graph Theory is that it is extremely
simple — at least at first — and it has few pre-requisites.
It reminds me of Boolean Algebra in this regard.

    ( en.wikipedia.org/wiki/Boolean_algebra_%28logic%29 )

I think you could easily teach this stuff, at least the introductory
material, to a clever 8-year-old.  I would use the analogy of cotton balls
connected by yarn.  You can move the balls and the yarn around all you like,
but the structure of the graph doesn't change.

                            * * * * * *

The early proofs in a Graph Theory text are remarkably intuitive.  Sometimes
it all seems so obvious and trivial, right up to the point where a powerful
theorem is proved.  For example, take the "Handshake Problem."

Imagine there's a bunch of people at a party, and all or some of them
shake hands.  Each handshake involves two people, no funny business,
no shaking hands with yourself, no three-way handshakes, etc.  We ask
everyone to keep track of how many different people they shake
hands with.  (If two people shake hands more than once, only count the
first handshake.)  Then everyone stops, and we ask for a show of hands
of all the people who shook hands an odd number of times.  It is possible
to prove that the number of hands raised must be even.  You can prove
this entirely with arithmetic and logic.

    ( mathforum.org/library/drmath/view/54292.html )

You can also map it onto a graph, with n nodes, one
per person, and an edge between each pair of nodes if those two
people shook hands.  Call the number of edges connected to each node the
degree of the node.  The number of nodes of odd degree will be even.

Now if you're talking about the old Bridges of Königsberg problem,
each node with an odd degree must be the start or endpoint
of a walk about the city.  Why?  Imagine someone is wandering the city,
vaccuming up edges which are marked in chalk on the pavement.  Every
time they pass through a node — which may or may not involve
a choice — they vaccum up two edges: the incoming and the outgoing.
The number of remaining edges goes down by two; if it's even it stays
even and if it's odd it stays odd.  If a node's degree is even it will
eventually drop to zero, it won't be visited again.  If its odd it
will drop to one, and if the traveler ends up there, they must stop.
(The only exception to this is the starting node, which will change from
odd to even or vice versa as the traveler begins vacuuming.)

So you see, if the graph of the seven bridges had zero or two nodes
of odd degree, the puzzle would've been solvable.  Zero odd nodes
would mean you could start anywhere (and end up where you started).
Two odd nodes would be the mandatory start and end points.  Depending on
how you draw it, the problem is usually represented by four odd nodes
(three of degree 3 and one of degree 5), so a single path across all
seven bridges is impossible.



illustration from Wolfram MathWorld
http://mathworld.wolfram.com/KoenigsbergBridgeProblem.html

                            * * * * * *

The sledding got rather tough in Haggard's book after the first excursion.
I was mucking about in "Excursion II, Ringel's Problem," when I turned
to Wikipedia for help.  I was having trouble with his definition of a
valuation applied to a tree (a tree is a graph with no cycles).  The whole
thing was just a little too terse, filled with mind-bending concepts expressed
mostly by formal definition, and with few examples.  Well, Wikipedia didn't
save me, directly, but it alerted me to the interesting coincidence that
"Ringel's Problem" came from Dr. Gerhard Ringel, who was teaching at the
University of California at Santa Cruz the entire time I was a student there,
doing original Graph Theory work, including during the Winter 1977 quarter
when I took "Graphs, Games and Structures" from his colleague Dr. David
Huffman and first learned this material.  I never met him, or even heard of
him to my recollection, but he'd coauthored a text on Graph Theory.  I bought
the latest edition of his book on Amazon and began reading it instead.

When I mentioned this on Facebook one of my friends remembered the author:


"Gerhard Ringel was my prof for graph theory at UCSC. The book we used
was also from him, but definitely a previous edition. Everyone in the
class called him Gerhard (typical for UCSC), but I always called him
Herr Doktor Ringel. I just read he passed away a few years ago. Sad.
I really enjoyed his class."


Knowing that another member of the older generation of Graph Theorists
had passed away, I approached this material with a new urgency.  It did turn
out that the newer book was less terse and had more examples.  It was
also more of a survey of the field than Haggard, which was basically
a set of representative puzzles in the field, so I switched to reading
Hartsfield and Ringel.  The ubiquity of Facebook in this story also
reaffirmed my conclusion that it is the dawn of a Golden Age of
Funding in Graph Theory.

                            * * * * * *

In the middle of this excursion a documentary DVD showed up from our Netflix
queue about Hungarian mathemitician Paul Erdös.  His life was a metalogue
of Graph Theory;

    ( en.wikipedia.org/wiki/Steps_to_an_Ecology_of_Mind#Part_I:_Metalogues )

he travelled around collaborating with other mathemeticians, and set the
record for the most collaborations.  The "Erdös Number" is named after
him — it's like a Kevin Bacon number for math.

    ( en.wikipedia.org/wiki/Erdos_number )

I was inspired to make this Facebook posting on July 17, 2012:


A nice visual illustration of a simple proof of a theorem
in graph theory, from the biography "Paul Erdos: N Is a Number"
— skip to 25:00. "Suppose we have six people at a party.
Then there are always three of them, so that either every two
know each other, or no two know each other. Is that clear?"

www.mashpedia.com/Paul_Erd%C5%91s



                            * * * * * *

Another simple theorem that just blew me away involved bipartite graphs.
These are graphs in which it is possible to divide all the nodes up into two
groups, like children playing "Red Rover" lined up on opposite sides of a
field, and have all edges cross the field between them.  In other words, if
you have nodes divided into the Red Team and the Blue Team, all edges go from
Red to Blue, and none go from Red to Red or Blue to Blue.

An example of this structure is the lists of actors and movies in the
Internet Movie Database (IMDB).

    ( www.imdb.com )

Ignoring extraneous stuff on ther web site, consider just the lists of movies
each actor has been in, and the list of which actors have been in each movie.
This is the network on which you overlay the game "Six Degrees of Kevin
Bacon."

    ( en.wikipedia.org/wiki/Six_Degrees_of_Kevin_Bacon )

It's a given that a movie can't act in a movie, and an actor can't act in
an actor, so each of the edges connect an actor to a movie.  Here is the
solution to "Buddy Ebsen to Buddy Hacket" which I originally gave in
"Six Degrees of Buddy Hackett" — note that going from an actor to
a movie and then to another actor counts as one degree of separation.


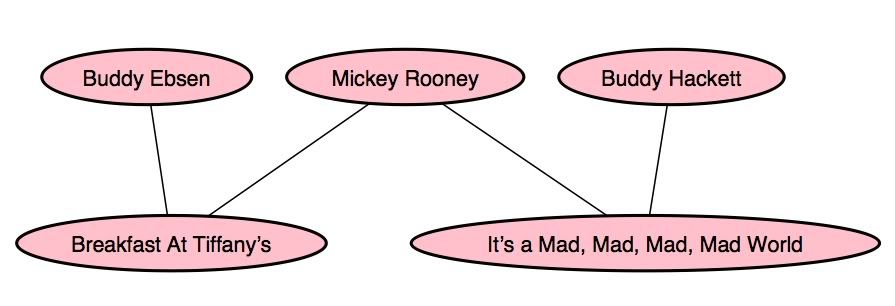Buddy Ebsen to Buddy Hacket in two degrees of separation
(each connecting edge is one-half of a degree of separation)

The above is an example of a bipartite graph.

Below is a complete bipartite graph; all three actors appear
in both movies, so all possible edges are drawn.


a fully connected bipartite graph of size K3,2 (images created with
GraphViz tools www.graphviz.org)

Notice that unlike the linkge between the Buddies, this one has potential
loops.  They're called cycles in Graph Theory, and if the number of
edges leading back where you started is even, it's an even cycle, otherwise
it's odd.  In the above graph there are three cycles you can trace of
length 4.  Can you find them?  (Hint: each involves skipping one actor.)
This leads to a theorem that boggled my mind when I first encountered it:

    A graph is bipartite if and only if it has no odd cycles.

It seemed "out of the blue" at first, but then I thought about.  What
if there was a "triangle," that is, a cycle of length 3?  At some point
you'd have to link an actor directly to another actor, or a movie to
another movie, to complete the triangle.  Similar arguments apply to
all other odd cycle lengths. There are a number of formal proofs on-line.

    ( www.proofwiki.org/wiki/Graph_is_Bipartite_iff_No_Odd_Cycles )

This also means a tree, which is a graph with no cycles, is always
a bipartite graph, because it has no odd cycles.

I began to see the power of this seemingly simple branch of math.

                            * * * * * *

One of the key abstractions of Graph Theory is that a graph can be represented
by a matrix.  This works out to quite the hat trick, because mathematicians
can hop back and forth between the two representations, using whichever one
is working better for the problem at hand.  Also, a computer can't make
much sense of a drawing of a graph (at least not yet, though things are
bound to change), but it can do all sorts of interesting calculations on a
matrix, and at Gigaherz speeds.

Sometimes Graph Theory allows the additional complexity of multiple edges
connecting two nodes, or an edge connecting a node to itself, or an edge
with directional arrowheads at one or both ends, but a simple graph
doesn't have any of these extras.  So if you make a matrix, or table, of
connectivity between the nodes of graph, listing each node both acoss on top,
and down the left side, with a value of 1 for a connection and 0 for no
connection, you will always see these patterns:

    

  1.  there are always all zeroes down the diagonal from upper left to lower
 right (no node conncts to itself)


  2.  no value greater than one (only single edges between nodes)


  3.  the matrix is mirror-symmetric down the diagonal from upper left to
 lower right (if node A connects to node B, node B also connects to node A;
 edges are always bi-directional)



For example, consider the graph with three nodes and three edges connected
in a triangle:



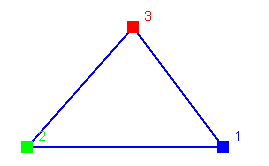
This matrix represents the same graph:




  1 2 3 


 1 0 1 1 


 2 1 0 1 


 3 1 1 0 




Note that except for the zeros on the diagonal, it'a all ones.  It's a
fully connected graph.

Next, consider this graph with four nodes:



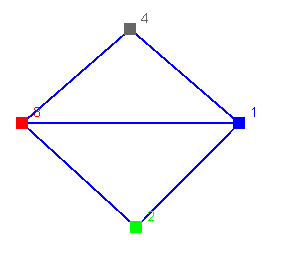
It's not fully connected.  There is no edge from node 2 to node 4 (or
vice versa).  Here is it's matrix:




  1 2 3 4 


 1 0 1 1 1 


 2 1 0 1 0 


 3 1 1 0 1 


 4 1 0 1 0 




Note that in additonal to zeroes down the diagonal, it has zeros in
row 2 column 4 and row 4 column 2.

If you add the missing edge you get this graph:



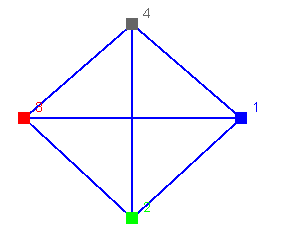
with this matrix:




  1 2 3 4 


 1 0 1 1 1 


 2 1 0 1 1 


 3 1 1 0 1 


 4 1 1 1 0 




Once you have a graph in matrix form, it's easy to answer certain questions.
What is the degree of each node?  Just add each row — or each column,
you get the same answers.  (Why?)

Can you do an Euler Walk and visit all the edges without repeating?
Well, how many nodes of odd degree are there?  If more than 2 then the
answer is no.

Making sense yet?

[Images taken from: "Graph Theory Lessons" at Math Cove.]

    ( www.mathcove.net/petersen/lessons/get-lesson?les=11 )


                            * * * * * *

Now for the most magical thing of all.  Once you have a graph in matrix
form, it is easy (though tedious — but that's what computers are for)
to compute the number of walks of any given length between any two nodes.
It's done with matrix multiplication, a standard part of the linear algebra
curriculum.  Nowadays a number of math packages can do it, including even
Excel and some other spreadsheets with a bit of cleverness.

The magic rule is:


If M is the matrix of a simple graph, MP will yield a matrix in
which the I,Jth number is the number of walks of length P
from I to J.


Here's an example (and I did use a computer to help me).

Take the triangle graph above.  Stripping the row and column markings
for simplicity, its matrix — call it T — is:

     0 1 1
     1 0 1
     1 1 0

This also happens to be T raised to the first power (an identity operator),
so each number tells us the number of walks of length one from I to J.
Which is the definition of an adjacency matrix, so no magic yet.

Now we take T squared, or T times T, which I'll write T^2:

T^2: 2 1 1
     1 2 1
     1 1 2

This matrix has the same symmetry as the original, which makes sense
because they're really no way to tell the three nodes apart except by name;
they all have degree two, and lead to other nodes of degree two.
But, to be complete, let's look at all nine entries in the matrix.
The upper left 2 is the number of walks of length 2 from 1 to 1.  The
two walks are: from 1 to 2 and back to 1, or from 1 to 3 and back to 1.
Follow along on any convenient triangle.  (This also makes a great puzzle
for kids.)  Here are the 12 walks of length 2 represented by the nine matrix
values:

walks from 1 to 1:
                   1) 1 -> 2 -> 1
                   2) 1 -> 3 -> 1
walks from 1 to 2:
                   1) 1 -> 3 -> 2
walks from 1 to 3:
                   1) 1 -> 2 -> 3
walks from 2 to 1:
                   1) 2 -> 3 -> 1
walks from 2 to 2:
                   1) 2 -> 1 -> 2
                   2) 2 -> 3 -> 2
walks from 2 to 3:
                   1) 2 -> 1 -> 3
walks from 3 to 1:
                   1) 3 -> 2 -> 1
walks from 3 to 2:
                   1) 3 -> 1 -> 2
walks from 3 to 3:
                   1) 3 -> 1 -> 3
                   2) 3 -> 2 -> 3

SO the matrix is giving us the right counts all the way through!
There's your magic.

So, now look at T cubed, or T times T times T:

T^3: 2 3 3
     3 2 3
     3 3 2

Again the symmetry is preserved, and it will be to infinity,
since there is nothing to break it.  Let's just look at the first
two entries in the first row, since all the others resemble them.
Walks of length three:

walks from 1 to 1:
                   1) 1 -> 2 -> 3 -> 1
                   2) 1 -> 3 -> 2 -> 1
walks from 1 to 2:
                   1) 1 -> 2 -> 1 -> 2
                   2) 1 -> 2 -> 3 -> 2
                   3) 1 -> 3 -> 1 -> 2

And by the time we get to T^4, it's starting to get a little cumbersome.

T^4: 6 5 5
     5 6 5
     5 5 6

Buy you can see, this makes it totally possible to automate the answer
"What's the shortest walk from A to B?" (or from Alice to Bob) for graphs
of arbitrary size.

                            * * * * * *

Well, that's all pretty interesting in an abstract way, but let's remember
what the real world problems are that people are trying to solve by revisiting
Graph Theory.  Someone in the Business Analytics department gets handed a
thumb drive with a bunch of data on a social network, such as all the people
who hit "like" on Facebook for the Farrell's Ice Cream page,

    ( http://www.facebook.com/pages/FARRELLS-ICE-CREAM-PARLOR/37815396901 )

and who their friends are, but anonymized somehow.  It's basically a huge graph.
What to do with it?


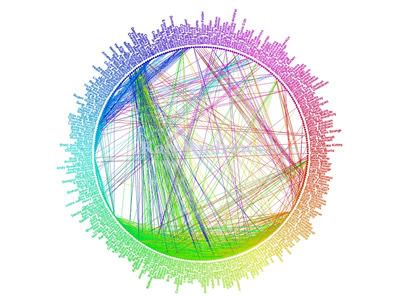a typical "friend wheel" — one person's
friends and how they interconnect
www.visualcomplexity.com/vc/project.cfm?id=501

Of course, what the marketing people want done is no less than figuring
out human behavior, and they're hoping this new data deluge will contain the
key.  I'm reminded of a story I kept hearing in the 1990s, at the dawn of
the dot-com era.  From a variety of sources I heard the tale of how 7-11
figured out that if they put beer next to the baby formula they sold more beer.
The explanation was that in the middle of the night Mom ran out of formula,
and she sent Dad to the 7-11 while she stayed home with the baby.  He saw the
beer next to the formula and grabbed a pack.  I was never able to get any
documentation on this, though, and sometimes the baby product changed to
diapers, and I figured it was an urban legend.  I especially wondered, how
did they know why it worked?  Where did they get their data?

More recently I read somewhere (I wish I could track this down) about a more
recently observed phenomenon: if you buy a car, people up to 3 degrees away
from you in your social network can be influenced to buy the same car, even
if you don't know each other, but people 4 degrees away not so much.
Nobody knows why exactly.  My reaction is "Welcome to the 21st Century."
From here on out we're going to find these weird things relating graph
structure and observed market behaviour, and nobody will know why.

But we may not need to.  Very recently a friend of mine who prides himself
on keeping up with high-tech developments told me about meeting someone
with a company that's making software to help pharamacutical sales people
by analyzing the social networks of doctors, hospitals and pharmacies they
sell to, and then suggesting an adoption order in which new treatments and
drugs can be introduced most succesfully.  Makes sense to me.  I've been
hearing this kind of analysis from senior sales people for years, done the
old fashioned way with Rolodex and brain power, but I believe some of it can
be teased out from digital records.

                            * * * * * *

You in the back with your hand up: What?  Something about ethical issues?
Well, consider that this kind of stuff is already going on, almost entirely
in secret.  I'm interested in promoting published or released information,
software, analysis, and science, and have faith that good things will
come from operating in the light.

In the near term I am working on a library of C language routines to
read, write, create, and analyze graphs, represented by text files
containing ones and zeros.

My plan is to release it someplace like Source Forge and see if people
find it useful.

I've written a first draft of the first program, to validate data.

    ( www.well.com/user/abs/ALL.validate_graph )

I'm looking for volunteer help, to extend the functionality, translate it
into Java, Javascript, PHP, C++, Objective C, C Sharp, Pearl, and Python,
and parallelize and optimizei it for "big iron."  I may have access to
cloud computing resources and even supercomputers.  Interested?

Here are some rough, fragmentary notes from my iPhone:



Graph Theory Lib

helper functions:
  mth_ordering(int n, int m) *
  multiply_square_matrices(int n, Graph a, Graph b)

graph creation:
  creat_graph(int n, string type, Graph a)
    (complete, complete_bipartite, line, cycle, tree, cube, wheel, windmill,
    Turan, random, ...}

graph analysis:
  validate_graph(int n, Graph a)
  graph_metrics(int n, Graph a, int results[]) *
    {vertex degrees, girth, diameter, density=edges/node, clustering? ...)
  compare_graphs(int n, Graph a, Graph b) *
  compute_graph_walks(int n, Graph a, int walk_length)
  find_graph_islands(int n, Graph a, Graph b)

graph operations:
  fix_graph(int n, Graph a)
  make_canonical(int n, Graph a) ?
  graph_union(int n, Graph a, Graph b, Graph c)
  graph_intersection(int n, Graph a, Graph b, Graph c)

* = don't yet know how
? = might know how




Book Review:
The Information: A History, A Theory, A Flood
(2012) by James Gleick


Claude Shannon and his maze-solving mouse
(upload.wikimedia.org/wikipedia/en/e/e5/Shannonmouse.PNG)



"We may say most aptly that the Analytical Engine weaves
algebraical patterns just as the Jacquard loom weaves
flowers and leaves."

    — Ada Lovelace
        Notes (1843)


This summer I was reminded that 2012 is the Alan Turing centennial.

    ( www.mathcomp.leeds.ac.uk/turing2012 )

Well, I can think of few better ways to celebrate than to read James Gleick's
new book, "The Information: A History, A Theory, A Flood."  It puts Turing's
work into context in a very approachable way, more so than the also excellent
"Gödel, Escher Bach: An Eternal Golden Braid" (1980) by Douglas R.
Hofstadter, which is more daunting,

    ( www.amazon.com/exec/obidos/ASIN/0465026567/hip-20 )

or the fascinating fictionalized "Cryptonomic" (1999) by Neal Stephenson, which
is more daunting and wanders more off-topic, being a novel and all.

    ( www.amazon.com/exec/obidos/ASIN/0380788624/hip-20 )

I picked up this book because James Gleick wrote it, and he also wrote
"Chaos: Making a New Science" (1988),

    ( www.amazon.com/exec/obidos/ASIN/0140092501/hip-20 )

which was a life-changing book for me, so I feel like I'd follow him anywhere.

Here Gleick grapples with the "big picture" in our 150-year transformation
from the Industrial Revolution to the Information Age.  (Interestingly,
the opening ceremonies of the 2012 Olympiad in London a few days ago dealt
with a similar theme, climaxing with a Tweet Heard Round the World from Web
inventor Tim Burners-Lee.)

    ( www.zdnet.com/uk/web-inventor-tim-berners-lee-stars-in-olympics-opening-ceremony-7000001744 )

Gleick takes us back to the invention of the telgraph, which obsolesced the
pony express and the semaphore line.

    ( http://en.wikipedia.org/wiki/Semaphore_line )


semaphore tower
from Wikimedia Commons

Despite being very sophisticated after centuries of scientific progress,
those working with these new inventions found it difficult to talk about
them.  The old terms didn't fit the new ideas.  What was sent by a telegraph
— or by a semaphor line — was not matter or energy, but some
new phenomenon consisting entirely of pattern.

Gelick proceeds to take us through Charles Babbage's invention of
the Analytical Engine, and his friend Ada Lovelace's attempts to
articulate its true nature.

We come to Claude Shannon at Bell Labs, inventing the "bit" as a measure
of this critter he calls "information" or "negative entropy."

Then it's on the famous Macy Foundataion meetings where the field
of "cybernetics" is said to have been invented.  His account of some of
the conversations at these meetings are no less than intensely evocative.
Overall his telling is less exhaustive and yet where it focuses attention
it is more detailed and gripping than the account in "The Cybernetics Group"
(1991) by Steve J. Heims.

    ( www.amazon.com/exec/obidos/ASIN/0262082004/hip-20 )

He proceeds to the struggle and controversy with recognizing the truly
digital nature of the genes encoded in the DNA molecule.

Along the way I saw shadows of the ideas of Gregory Bateson, to which
Gleick must have referred in researching his book.

When I studied under Bateson at UCSC, he liked to use the terms
Creatura and Pleroma which he'd gotten from  Carl Jung's essay
"Seven Sermons To the Dead" (1946), published as an appendix in the
autobiographical "Memories, Dreams, Reflections."

    ( www.amazon.com/exec/obidos/ASIN/0679723951/hip-20 )

They are Latin words taken from Gnostic writings.  Bateson called
Pleroma the world of forces and impacts, while Creatura
was the world of beings and messages.  Before the Information Age
people mostly only knew how to talk about cause and effect in terms
of the Pleroma.

Bateson also used to strain our brains by asking us to imagine what was like
to live before a given idea existed, and to not be able to think about
that idea.  There was a book on his reading list called "The Idea of
History" (1946) by R. G. Collingwood.

    ( www.amazon.com/exec/obidos/ASIN/0192853066/hip-20 )

It explained that it wasn't pretty much until the early Greeks that anybody
had an idea of "history," that you should write down what happened, and
when and where, to who, and file it away someplace.  Before that there
were religious tales, legends, heroic epics but not much in the way of facts.
Bateson challenged us to think about the pre-history of the idea of history.
(It was almost as weird as those physics professors who got me wondering what
went on before the beginning of time.)

Later, I taught a student-directed seminar at Kresge College, UCSC,
called "Whole Systems," and for the final class I had both Stewart Brand and
Gregory Bateson as guest speakers.  (Bateson's secretary Judith Van Slooten
was also there, now that I think of it, because we had a pot luck and Dixie
and I brought ox tail soup — a recipe Bateson had taught — and
Judith saved a ring-shaped tail bone and made it into a necklace.)

After a rousing discussion of how the study of whole systems looked
from our vantage point in time, the winter of 1975, Bateson said, "You
know thirty years ago we couldn't have this conversation."  A room
full of intelligent students and teachers who understood concepts
such as feedback loops, homeostasis, coevolution, and computer viruses
was much harder to find in 1945.  I thought about that for a while.

The tour de force that Gleick offers here is a series of glimpses
into these points in our recent history where people were first figuring
out how to "have these conversations."  As an introduction to informational
thinking it definitely works.

I would go so far as to add this book to my short list of books I would
use for an introductory Cybernetics class for grades 10 through 14.  That
list includes:

And I would start the first semester with Gleick's book.  It acts as a
bridge from the industrial assumptions of most of our schools and the
cyberspace environment hiding in the students smart-phones.

But one last concern: if it's all about sending "bits not atoms" over our
networks (as Nicholas Negroponte kept insisting in the early 1990s, writing
in WIRED Magazine at the dawn of the Internet), then why does the Kindle
edition of "The Information" cost more than the paperback?


Feature:
"If It's Just a Virtual Actor,
Then Why Am I Feeling Real Emotions?"
(Part Four)

mask



(If you haven't read parts one through three, see the archives, listed at the end.)


I'M READY FOR WHAT'S NEXT



"This is UTV, for you the viewer!"

    — The Firesign Theatre
        Don't Crush That Dwarf, Hand Me the Pliers
        (comedy album, 1970)


        ( www.amazon.com/exec/obidos/ASIN/B003W77SHG/hip-20 )

        ( en.wikipedia.org/wiki/Don%27t_Crush_That_Dwarf,_Hand_Me_the_Pliers )


"We called it 'stealing from the thieves.'  And when they started stealing
it back, we knew it was time to stop."

    —Bono
        "U2 - Zoo TV Live From Sydney" (Limited Edition) (1992)


        ( www.amazon.com/exec/obidos/ASIN/B000HEZC7U/hip-20 )

I rarely go to rock concerts, but in retrospect I realized I would've really
enjoyed the Zoo TV Tour by Irish rock band U2, which started at Lakeland,
Florida on 29 February 1992 and ended at Tokyo, Japan on 10 December 1993,
after 157 shows.

    ( en.wikipedia.org/wiki/Zoo_tv )

From what I've seen on video of this tour, it wasn't so much a concert as a
piece of interactive video performance art with rock music accompaniment.

    ( www.youtube.com/watch?v=QO6Bk1GMDLY )

I think the band's original concern was that they were moving from indoor
hockey arenas to outdoor football stadia on this tour, and they didn't want
the folks in the nosebleed seats to have a bad show, so they set up these giant
television monitors.  But as they began to expore the possibilites, including
live cameras on the band and the audience, mixed in with satellite feeds
from around the world, they began to craft an interactive video collage
that was different every time they performed it.

As they were rehearsing in Michigan, Kurt Loder of MTV News sniffed them
out and asked for an interview.  The band made him inverview their video
images on a giant screen, sort of like a "Wizard of Oz" moment.  Loder
played along.


Kurd Loder, MTV News: "One of the things about rock 'n roll stars is that
    they're bigger than life, they're bigger than the audience; they're almost
    intimidating.  Well, this whole set is like that. Right?"
Bono, U2: "That's right, yeah!"
Loder: "Isn't that — isn't that off putting, doesn't that kill intimacy though?"
Bono: "It does, absolutely.  But you look great!"


    ( www.youtube.com/watch?v=-VoGiXZUiNA&playnext=1&list=PLE2873FF957793C42 )

At the end Bono is grinning in his "Fly" shades on the giant screen, all icon.

There was a recurring prank in the show, as Bono persisted in calling U. S.
president George H. W. Bush from the stage, though Bush never took his call.

    ( www.youtube.com/watch?v=UmgYzASFZPU&feature=related )

One night Bono called presidential candidate Bill Clinton, who was after Bush's
job in 1992.  Clinton took the call.  The crowd went wild!

A non-recurring joke ocured when Dana Carvey, performing as the character
"Garth" from "Wayne's World" while hosting the 1992 MTV Music Video Awards,
linked up via satellite with U2 at a Detroit concert venue, and ended
up playing along on drums with "Even Better Than the Real Thing."

    ( www.youtube.com/watch?v=7UuKVtpiw9g )

But first "Garth" had to razz Bono by asking him if he ate Lucky Charms,
and then offering an apology: "I don't mean to bug ya'," a reference to
one of Bono's ironic political raps in the song "Silver and Gold."

    ( www.youtube.com/watch?v=-9NaIYULk6s )

On a more sombre note, the band did satellite video hookuops with citizens
of Sarajevo while it was under seige, drawing attention to the plight of
its residents.

I've long believed that artists act as a hypersensitive look-ahead system
for our civilization.  American author and humorist Kurt Vonnegut, Jr., called
them "canaries in a coal mine," and Canadian media analyst Marshall McLuhan
called the "our Defence Early Warning (DEW) system."

In 1992 there was a sea change in the culture, when a bunch of folks
became a lot more xenophillic (loving the strange) than before, and
ready to embrace change.  Virtual reality and telepresence were new
buzz words.  Computer Generated Imagery (CGI) was about to break through to
the mainstream in Hollywood.  Interactive entertainment was considered
by some the "next big thing."  The internet was about to get really big.
U2 saw some of this coming.  Here are some lyrics from the song that opened
almost every concert performance in the tour, "Zoo Station."

    ( www.youtube.com/watch?v=fMneYa8gJBY )



I'm ready
I'm ready for the laughing gas
I'm ready
I'm ready for what's next
I'm ready to duck
I'm ready to dive
I'm ready to say
I'm glad to be alive
I'm ready
I'm ready for the push
The cool of the night
The warmth of the breeze
I'll be crawling 'round
On my hands and knees

  * * * * * *

I'm ready
I'm ready for the gridlock
I'm ready...to take it to the street
I'm ready for the shuffle
Ready for the deal
Ready to let go of the steering wheel
I'm ready
Ready for the crush

  * * * * * *

Time is a train
Makes the future the past
Leaves you standing in the station
Your face pressed up against the glass



IT'S THE INTERTACTIVITY, STUPID



"Tele-TV was the prototype of a deal for a company with more money
than media-market savvy.  The deal was sold to Pacific Bell, NYNEX,
and Bell Atlantic by Michael Ovits, perhaps the most influential
agent in the entertainment industry at the time."

    — John Handley, 2005
       "Telebomb: The Truth Behind the $500-Billion Telecom Bust
       and What the Industry Must Do to Recover"



            ( www.amazon.com/exec/obidos/ASIN/0814408338/hip-20 )

I never made it to the Zoo TV Tour in person, but I watched a lot of the
videos later.  I remember thinking that if I ever met any members of the
band, I would tell them about the interactive paddles I saw at SIGGRAPH '91
in Las Vegas, shown by Loren Carpenter of PIXAR in the Electronic Theater, and
suggest they could use this technology in their live shows, to let the
audience participate more.  (This technology is now commercially available from
Cinematrix.)

    ( usa.cinematrix.info )

Bill Clinton won his election in November of 1992.  They say he had a banner
in each campaign headquarters that said, "IT'S THE ECONOMY, STUPID!"  This
inspired me to coin the slogan, "IT'S THE INTERTACTIVITY, STUPID!"

One of things that was sort of fun to watch at that time was how hysterical
the Old Media companies were getting about missing the boat in interactive
media.  It was a moving target.  First it was interactive CD-ROMs, and
everybody was getting Media Kit upgrades for their PCs (CD-ROM drive, sound
card, speakers) to be able to play them.

(Recently I found and played an interactive CD-ROM about David Bowie.  Gawd,
it sucked.  They wouldn't let me steer!  I had go through their garden
path and wait for their crappy shovelware, low bandwidth video and
miniscule inside information.  What a yawn.)

Then suddenly about early '93 that wasn't it, the CD-ROM was dead,
and TV Set-Top Boxes were the new holy grail of interactive entertainment.
A thousand channels!  Pick your camera view in a basketball game!
Vote on the plot of a soap opera!  Order stuff!  Now that was a biggie.
The Firesign Theatre parodied this in a direct-to-video feature called
"Nick Danger In the Case of the Missing Yolk" (1989)

    ( www.amazon.com/exec/obidos/ASIN/630293348X/hip-20 )

in which the hapless yokels in the Yolk family get an interactive TV
and then make a series of poor retail choices from the couch.  Hilarity ensues.

Cable and phone companies, on the one hand, and movie/TV content providers
on the other began to team up in strategic alliances.  But nobody could figure
out how to get the consumer to pay $600 for a monopolistic box.

One important thing I think they were missing is the amount of
interactivity.  It is possible to measure these things.  We measure the
Baud Rate of the data coming down in Kilobytes or Megabytes per Second.
If you're a Yolk on the couch with a button, you got maybe 1 or 2 Bits
(not Bytes) per second going upstream.

People want more than that.  They want to jump up and down and wave their
arms and shout and play air guitar and press pedals and fire virtual guns
and make a lot of things happen.  They want to steer.  Trust me on this.
It was true in 1993 and it's even more true in 2012.

STAGE DOOR JOHNNIES


character Mandora from the Adventurer's Club
advclub.wikia.com/wiki/Mandora



"The maid is the only character in the club to have a unique identity
when played by a different actress (by way of contrast, 'Graves' is
always known as 'Graves' no matter which actor is playing him). Past
and present maids include 'Anelle', 'Yvette', 'Sugar Snap', 'Beullah
Belle', 'Ginger Vitus', 'Sunny Knight', 'Kiki McGee', 'Gabby Normal',
'Tish Myash', 'Dusty Cabinets', 'Tallulah Buttertart', 'LaRue ',
'Molly McClean' and more."

    — Wikipedia article on "The Adventurers Club"

            ( en.wikipedia.org/wiki/Adventurers_Club )

By this time my standards for interactive entertainment were pretty high.
I'd seen "buskers" (street performers) in Balboa Park, San Diego, California,
in Harvard Square, Cambridge, Massachusetts, and on the Pacific Garden Mall
in Santa Cruz, Calfornia, doing some pretty remarkable things, and I'd also
been to the Adventurers Club [op. cit.] a number of times.  I wasn't
going to be impressed by picking my camera angle.

And there was a secret weapon that the buskers and the Adventurers
shared: sexy sells, and interactively sexy sells even better.  Now,
nowbody's being obscene here, there's just a hint.  And the interactive
artists can adjust that level, which can yield fascinating results.
The early show can be more kid-friendly, and the converse as well.

When I first started visiting the Adventurers Club, there was a very
sexy character named Mandora, who was an adventurer and a cabaret singer.
She flirted with the guys and showed a little skin.

    ( www.youtube.com/watch?v=cXeGtnIYNHc )

Well, the fellers were all over her like flies on pancake syrup.  I guess
around 1959 a lounge singer in a boa could rub a bald headed guy's scalp
while singing a torch song, and he'd turn beet red, and the audience
would roar, but by the '90s he'd be more likely to hang around the stage
door after the show, which becomes a security problem.  Soon Mandora was
gone, replaced by the toned-down Samantha Sterling, who was an adventurer
but not a cabaret singer (though she did sing in the caberet, actually)
and showed less skin and didn't flirt as much.  There were still a few
security problems.  For all I know that sort of thing is why the club
was eventually closed.

To tell you the truth, I had a bit of "thing" for Mandora myself, which
was kind of confusing, because even though she was a living, breathing woman
right in front of me, she was also a fictional character.  The interactivity
threw me off.  I also favored one actress over another, so I felt like
only one was "my" Mandora.  I also was very fond of her maid character,
Ginger Vitus.  This seems weird to relate after all these years.

I'm not the only one who's noticed the strange quasi-relationships
people form with actors and characters in their entertainments.
Critic David Thomson points out in "The Whole Equation: A History
of Hollywood" (2004),

  ( www.amazon.com/exec/obidos/ASIN/0375400168/hip-20 )

that spouses rarely get jealous if you say you have a crush on a big movie
star.  He confesses to being very attracted to Nicole Kidman, and expresses
amazement that as a critic he is permitted to write that in his columns
and nobody blinks twice.

In my case I eventually took my wife to see the actress, now playing
Samantha Sterling, and we together managed to bypass any security red flags
that might otherwise get raised and take her out to breakfast, but that's
getting ahead of the story.


TO BE CONTINUED...





========================================================================
newsletter archives: 
    www.well.com/user/abs/Cyb/archive 

========================================================================
Privacy Promise: Your email address will never be sold or given to
others.  You will receive only the e-Zine C3M from me, Alan Scrivener,
at most once per month.  It may contain commercial offers from me.
To cancel the e-Zine send the subject line "unsubscribe" to me.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I receive a commission on everything you purchase from Amazon.com after
following one of my links, which helps to support my research.
========================================================================
Copyright 2012 by Alan B. Scrivener
Last update: Wed Aug 1 00:51:08 PDT 2012