======================================================================== Cybernetics in the 3rd Millennium (C3M) Volume 10 Number 3, Nov. 2012 Alan B. Scrivener — www.well.com/user/abs — mailto:abs@well.com ======================================================================== In this issue:

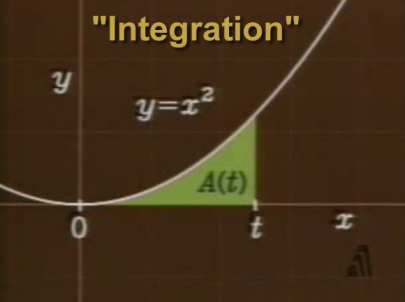
screen shots from Caltech's "The Mechanical Universe" en.wikipedia.org/wiki/The_Mechanical_Universe
- Short Subjects
- Teaching Calculus to a Sixteen-Year-Old
- Note Re: "If It's Just a Virtual Actor, Then Why Am I Feeling Real Emotions?"
Short Subjects: Bateson Documentary in LA; WELL Update; 'Steps...' On-line; Reading List

Bateson Documentary in LA
SHORT NOTICE! Posted on Nora Bateson's Facebook page yesterday:From: Earl Crabb <esoft@well.com> For my friends in the Los Angeles area... Nora Bateson provides a screening of her film -- An Ecology of Mind -- a film about her father Gregory Bateson and the relevance of his thought to our day. Monday, November 5, 2012 at 7:00 p.m. Art Center College of Design Hillside Campus - Los Angeles Times Media Center 1700 Lida Street, Pasadena, CA 91103 After the film screening, she will be there for a discussion and Q&A session. More like Q&Q.. I am alergic to answers. More info contact: cwilley@artcenter.edu
WELL Update
I got this email recently:From: Earl Crabb <esoft@well.com> Subject: The WELL now owned by The Well Group, Inc. Date: September 20, 2012 4:58:02 PM PDT To: Alan Scrivener <abs@well.com> Dear abs, We did it! We now own The WELL -- lock, stock and domain name. The joint press release with Salon is posted in the news conference. In addition, there is a topic, also in the news conference, for questions and answers. For you, things should operate as they always have, but if you discover any issues, please send email to helpdesk@well.com, just as always. How did this happen? It was the unbelievable show of member support, plus the member pledges, that empowered the investor group of WELLperns to make the offer accepted by Salon Media Group. It was Salon that sold us to us, because keeping this community together was a priority to them. Now, every single member of the WELL can take a bow, pop the champaign, and celebrate. You will not see any changes to the service that you currently receive (a "seamless transition" as the suits would say). But first let's take a moment and please accept my gratitude. We couldn't have done it without all of us. Thank you!! And Whoo-hoo! Earl Crabb CEO, The Well Group, Inc.So it looks like I can keep my email address and web site until the next disruption. Thanks for the support.
'Steps...' On-line
Not sure how or why, or the legality, but a full PDF copy of Gregory Bateson's "Steps To An Ecology of Mind" has appeared on-line at Scribd. ( www.scribd.com/doc/58544877/Gregory-Bateson-Steps-to-an-Ecology-of-the-Mind )Reading List
 burning book cake from
butterybooks.com
burning book cake from
butterybooks.com
"You don't have to burn books to destroy a culture. Just get people to stop reading them." — Ray Bradbury (in honor of his passing this year, the new HTTP error code 451 was introduced, for items blocked by government censorship)Since our last issue, I found another four books with bookmarks in them:
- Rafell, Burton [trans.] Sir Gawain and the Green Knight (c. 1375-1400) ( www.amazon.com/exec/obidos/ASIN/0451626249/hip-20 )
- Huxley, Aldous Crome Yellow (1921) ( www.amazon.com/exec/obidos/ASIN/1466285397/hip-20 )
- Von Foerster, Heinz [ed.] Cybernetics of Cybernetics (1974) ( www.amazon.com/exec/obidos/ASIN/0964704412/hip-20 )
- Hannum, Robert C. and Cabot, Anthony N. Practical Casino Math — Second Edition (2005) ( www.amazon.com/exec/obidos/ASIN/0942828534/hip-20 )
- Lewis, Michael Next: The Future Just Happened (2001) ( www.amazon.com/exec/obidos/ASIN/0393323528/hip-20 )
- Girard, Joe Joe Girard Complete Audio Box Set CD (2006) ( www.amazon.com/exec/obidos/ASIN/006087709X/hip-20 )
- Collins, Jim Good to Great: Why Some Companies Make the Leap... and Others Don't (2001) ( www.amazon.com/exec/obidos/ASIN/0066620996/hip-20 )
- De Kehoe, Joe The Silence and the Sun: An Historical Account of the People, Places and Events on Old Route 66 and Railroad Communities in the East Mojave Desert, California (2007) ( www.amazon.com/exec/obidos/ASIN/097938270X/hip-20 )
- Borneman, Walter R. Rival Rails: The Race to Build America's Greatest Transcontinental Railroad (2010) ( www.amazon.com/exec/obidos/ASIN/140016768X/hip-20 )
Teaching Calculus to a Sixteen-Year-Old
 a page from "Prof. E McSquared's Calculus Primer"
( www.amazon.com/exec/obidos/ASIN/0971462402/hip-20 )
a page from "Prof. E McSquared's Calculus Primer"
( www.amazon.com/exec/obidos/ASIN/0971462402/hip-20 )
"And what is the use of a book," thought Alice, "without pictures or conversation?" — Lewis Carroll, Alice in WonderlandOn several occasions I've bragged that I could teach calculus to middle school students, as long as I could skip limits and avoid proofs, and could use computers. (I especially wanted to avoid limits because I think the fundamental math behind them is vaguely fraudulent, not unlike the Induction Theorem, and I've found these kind of shenanigans always cause some students to drop out of math, though they usually can't articulate why.) Two summers ago my daughter, then 16, called my bluff. She wasn't taking summer school for the first time in a while, and asked me to teach her calculus, so I put together 11 lessons over about 7 weeks. I'd say it was a success, and I've since been asked to reveal my curriculum, so here goes. First I should say a few words here about how I learned math, and how I taught our daughter.
How I Learned Math
I was always bored in school, so I would often sit and read. The school library set up a little annex at the back of the classroom, so I had some pretty okay books. I loved books on magic, puzzles and tricks, and math puzzles and recreations. I managed to stay ahead of the math curriculum by reading. As a result, nothing in math class was ever a complete surprise to me. It all made more sense if I'd encountered it before. I'm certain this was instrumental in my high grades and test scores in math. This momentum did not break down until I was a freshman in college, and exposed to the temptations of hitch-hiking to Oregon to hang out with some way cool friends who ate great organic food and lived in this big house that had a belfry, plus an old couch and a bunch of old National Lampoons on the front porch. When they found out I had never been drunk they broke out the frozen daiquiri kit and some very interesting things happened. But I digress. When I returned from this jaunt I took a Caluclus 3 final and encountered the Del operator on the test, which I had never laid eyes on before. ( en.wikipedia.org/wiki/Del_operator ) It looked like an upside-down triangle. I was staring at stuff like this in panic: |
How I Taught Our Daughter
When I was in high school I started a binge of reading books on advances in education, and I soon came to the delightful books by James Herndon. His How to Survive in Your Native Land (1971) ( www.amazon.com/exec/obidos/ASIN/0867094087/hip-20 ) is an affable manifesto on what it looks like is wrong with education from a teacher's point of view. At one point he described a survey article he read by some researchers who looked at all the ways scientists had tried to increase the intelligence of rats, and which ones had worked. Their conclusion was that the only reliable way to increase the intelligence of rats was to let them roam freely in a complex and varied environment. This became my main educational strategy. Our house was always filled with the best educational stuff we could find, and we never made her play with any of it. It was just there, and sometimes we'd make helpful suggestions when she was bored. We made sure the house had several computers, PCs and MAcs, with games she would enjoy, and over time she became expert at troubleshooting common comuputer problems. I also made it a point to track educational games and pasttimes, especially when recommended by Martin Gardner ( en.wikipedia.org/wiki/Martin_gardner ) or Raymond Smullyan. ( en.wikipedia.org/wiki/Smullyan ) Bridg-It game shown at Boardgame Geek
boardgamegeek.com/boardgame/11052/bridg-it
For example, Gardner recommended an old board game from the 1960s called
"Bridg-It," originally invented by communications theory pioneer Claude Shannon.
I found one on eBay. It was fun at parties.
( en.wikipedia.org/wiki/Shannon_switching_game )
To help our daughter avoid math anxiety, I made up a series of math games for
her to play starting about age 3. I don't have room to detail them here,
but one day I hope to write a book about this called "How To Raise a Genius
in Ten Easy years."
This approach worked very well; she has always done well in math. (She did tell
me as a pre-teen that there were actually 2 kinds of math, the fun daddy math
and the boring school math.)
Another lesson I learned from Herndon was "make them take it away from you."
In one of his books he describes how he got his middle school students to make
a film. He showed up at school with a camera and started shooting. He wouldn't
explain and he wouldn't share. They finally dragged it out of him that he'd been
loaned the camera and given the film stock so he could use them in his teaching.
They figured that meant he shoud let the kids participate, and pretty soon they
had a plan "for the movie" and eventually they kicked him off the project.
This worked smashingly for us. For example, my daughter begged me to let her play
with iMovie on my old clamshell Mac, and when I finally gave in she became an
accomplished editor in no time.
So, naturally, I was ecstatic that she wanted calculus lessons. It may have been
a high point of my life. But I played it cool. I prepared about an hour of
material for each lesson, and told her when I had it ready, and then I waited for her
to tell me when she wanted the session. There was no pressure, and everything was
voluntary and on-demand.
By way of background, I should mention that she had completed Algebra I and II
in the California high school curriculum.
Bridg-It game shown at Boardgame Geek
boardgamegeek.com/boardgame/11052/bridg-it
For example, Gardner recommended an old board game from the 1960s called
"Bridg-It," originally invented by communications theory pioneer Claude Shannon.
I found one on eBay. It was fun at parties.
( en.wikipedia.org/wiki/Shannon_switching_game )
To help our daughter avoid math anxiety, I made up a series of math games for
her to play starting about age 3. I don't have room to detail them here,
but one day I hope to write a book about this called "How To Raise a Genius
in Ten Easy years."
This approach worked very well; she has always done well in math. (She did tell
me as a pre-teen that there were actually 2 kinds of math, the fun daddy math
and the boring school math.)
Another lesson I learned from Herndon was "make them take it away from you."
In one of his books he describes how he got his middle school students to make
a film. He showed up at school with a camera and started shooting. He wouldn't
explain and he wouldn't share. They finally dragged it out of him that he'd been
loaned the camera and given the film stock so he could use them in his teaching.
They figured that meant he shoud let the kids participate, and pretty soon they
had a plan "for the movie" and eventually they kicked him off the project.
This worked smashingly for us. For example, my daughter begged me to let her play
with iMovie on my old clamshell Mac, and when I finally gave in she became an
accomplished editor in no time.
So, naturally, I was ecstatic that she wanted calculus lessons. It may have been
a high point of my life. But I played it cool. I prepared about an hour of
material for each lesson, and told her when I had it ready, and then I waited for her
to tell me when she wanted the session. There was no pressure, and everything was
voluntary and on-demand.
By way of background, I should mention that she had completed Algebra I and II
in the California high school curriculum.
Lesson 1 — 24 June 2010
At the beginning I told her that I was going to follow the approximate sequence of material in a previous issue of C3M, volume 6 number 1, "Everything Has To Go Somewhere ~ OR ~ Eigenvectors and You" from January 2007, in case she wanted to refer to it during the class or later on. ( www.well.com/user/abs/Cyb/archive/c3m_0601.html ) Next I drew a little diagram to show how math has been traditionally done through ages, contrasted with how it needs to be now that we have cheap computers.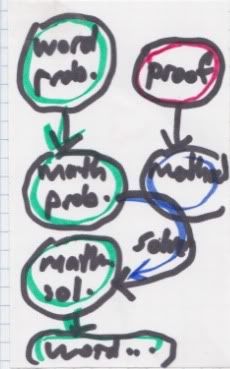 In the old days things worked like this: Mathemeticians would create one or more
proofs, which enable methods for solving problems, as shown by the red and
blue circles on the right side. Later, someone cames along with a problem, initially a
word problem, and they proceeded to convert it to a math problem, then use the
method to solve the problem, then convert the math solution into a word solution.
In educating students, we taught them the proofs so they'd be well-rounded, or
something, as well as the methods so they could solve problems.
Well now you don't need the proofs or the methods, I explained. Symbolic solvers
like Mathematica from Wolfram Research
( www.wolfram.com/mathematica )
can solve most the equations anyone will ever encounter, so we can concentrate on
translating between words and math and back. But we still need to understand
the concepts!
Here is the roadmap I laid out. I planned to cover:
In the old days things worked like this: Mathemeticians would create one or more
proofs, which enable methods for solving problems, as shown by the red and
blue circles on the right side. Later, someone cames along with a problem, initially a
word problem, and they proceeded to convert it to a math problem, then use the
method to solve the problem, then convert the math solution into a word solution.
In educating students, we taught them the proofs so they'd be well-rounded, or
something, as well as the methods so they could solve problems.
Well now you don't need the proofs or the methods, I explained. Symbolic solvers
like Mathematica from Wolfram Research
( www.wolfram.com/mathematica )
can solve most the equations anyone will ever encounter, so we can concentrate on
translating between words and math and back. But we still need to understand
the concepts!
Here is the roadmap I laid out. I planned to cover: - differential calculus
- integral calculus
- mechanics
- Ordinary Differential Equations (ODEs)
- Finite State Machines (FSMs)
- systems theory
- Mechanical Universe
- textbook, 1986, by Steven C. Frautschi, Richard P. Olenick, Tom M. Apostol, David L. Goodstein * ( www.amazon.com/exec/obidos/ASIN/0521304326/hip-20 )
- videos, 1985, by Dr. David Goodstein, Jim Blinn, Peter F. Buffa, Mark Rothschild ( www.amazon.com/exec/obidos/ASIN/B0027K9UES/hip-20 ) ( www.learner.org/catalog/series42.html ) ( www.phys.ufl.edu/demo/demobook/MechUniv/MechU.html )
- Prof. E McSquared's Calculus Primer (comic book, 1974) by Swann Howard ( www.amazon.com/exec/obidos/ASIN/0971462402/hip-20 )
- An Introduction to Cybernetics (book, 1966) by Ross Ashby ( www.amazon.com/exec/obidos/ASIN/B001TC7UVA/hip-20 )
- Excel spreadsheet software from Microsoft Corp. * ( www.amazon.com/exec/obidos/ASIN/B0039L2XG6/hip-20 )
- Google Docs spreadsheet software from Google Corp. ( docs.google.com )
- GNU Octave free software (Matlab work-alike) from the Gnu Foundation * ( www.gnu.org/software/octave )
- the Application Visualization System version 5 (AVS5) software from Advanced Visual Systems Inc. (AVS Inc.) ( www.avs.com/products/avs5/index.html )
- the C programming language ( en.wikipedia.org/wiki/C_programming_language )
- the Collosal Cave text-based Adventure game ( en.wikipedia.org/wiki/Collosal_Cave_Adventure )
- the Wikipedia collaborative encyclopedia ( en.wikipedia.org )
- the Wolfram Alpha web site, which provides an augmented front-end to Mathematica ( www.wolframalpha.com )
- the text-based units program on many UNIX systems ( www.gnu.org/software/units )
- the text-based basic calculator (bc) on most UNIX systems ( linux.die.net/man/1/bc )
- Isaac Asimov's science and math essays from Fantasy and Science Fiction (S&SF) * ( www.asimovonline.com/oldsite/Essays/f_and_sf_essays.html ) ( www.amazon.com/exec/obidos/ASIN/0671821342/hip-20 )
- Ralph Abraham and C. D. Shaw's so-called "chaos comix," Dynamics, the Geometry of Behavior (1992) ( www.amazon.com/exec/obidos/ASIN/0201567172/hip-20 ) ( www.aerialpress.com/DYN/DYN4Pt1Ch0X.pdf )
 |
Lesson 2 — 25 June 2010
concepts:- constant acceleration ( en.wikipedia.org/wiki/Constant_acceleration#Uniform_acceleration )
Lesson 3 — 28 June 2010
concepts:- function ( en.wikipedia.org/wiki/Function_%28mathematics%29 )
- transform ( en.wikipedia.org/wiki/Transform_%28mathematics%29 )
- derivative ( en.wikipedia.org/wiki/Derivative )
- D: 1
F: 2
D: 2
F: 4
D: 3
F: 6
D: It's always twice as much!
D: 1
F: 7
D: 2
F: 7
D: 3
F: 7
D: It's always seven!
D: 1
F: 1
D: 2
F: 4
D: 3
F: 9
D: I don't know.
F: It's the number squared, you know, the number times itself.
D: Right!
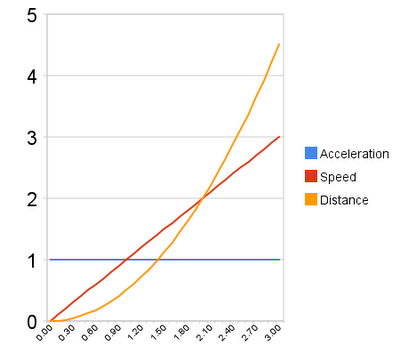 illustration for Betsy's Devine Algebraic Limerick,
from pergelator.blogspot.com
I told her there are Differentiation Rules for doing that transform we call differentiation,
and showed her the polynomial or elementary power rule as an example.
( en.wikipedia.org/wiki/Differentiation_rules )
This was how, for example, we took the derivative of 16*t^2 and got 32*t.
Next I showed how we could use the UNIX programs basic caluclator (bc) and units
to solve some simple problems for us. Invoking bc with its math library (what I typed is
in green):
illustration for Betsy's Devine Algebraic Limerick,
from pergelator.blogspot.com
I told her there are Differentiation Rules for doing that transform we call differentiation,
and showed her the polynomial or elementary power rule as an example.
( en.wikipedia.org/wiki/Differentiation_rules )
This was how, for example, we took the derivative of 16*t^2 and got 32*t.
Next I showed how we could use the UNIX programs basic caluclator (bc) and units
to solve some simple problems for us. Invoking bc with its math library (what I typed is
in green):
- % bc -l
bc 1.06
Copyright 1991-1994, 1997, 1998, 2000 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'.
scale=4
16*.1*.1
.1600
16*.5*.5
4.0000
16*1.5*1.5
36.0000
^D
%
- % units
586 units, 56 prefixes
You have: 14000 feet/second
You want: miles/hour
* 9545.4545
/ 0.0001047619
You have: ^D
%
 definition of differentiation illustrated at
www.splung.com/content/sid/1/page/differentiation
definition of differentiation illustrated at
www.splung.com/content/sid/1/page/differentiation
Lesson 4 — 29 June 2010
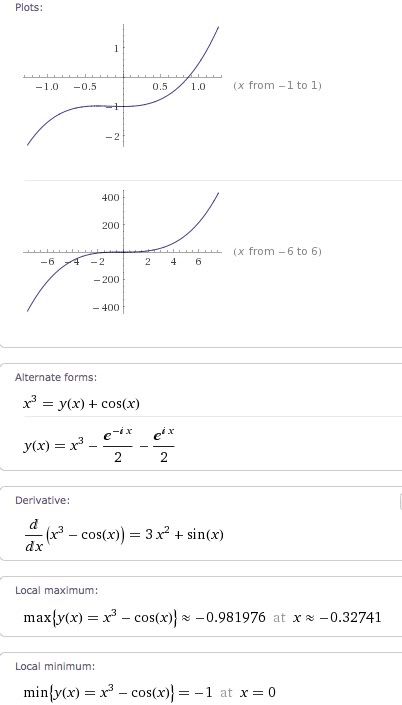
concept:- computer algebra system (symbolic solver) ( en.wikipedia.org/wiki/Symbolic_solver )
- y(x) = x^3 - cos(x)
- 3 x^2 + sin(x)
 I think we watched Mechanical Universe Epsiode 4: "Inertia" (28:36) and discussed it.
( video.google.com/videoplay?docid=4785917973509844622 )
I think we watched Mechanical Universe Epsiode 4: "Inertia" (28:36) and discussed it.
( video.google.com/videoplay?docid=4785917973509844622 )
Lesson 5 — 2 July 2010
concepts:- utility function ( en.wikipedia.org/wiki/Utility_function )
- minimum and maximum ( en.wikipedia.org/wiki/Minimum )
- vectors ( en.wikipedia.org/wiki/Vector_%28mathematics_and_physics%29 )
 crude diagram (please ignore bad algebra)
Variable x the thing we have control over, in this case the position of the factory
along the road from -5 to 5, and the utility function u(x) represents dollars in revenue
we would like to maximize, or dollars in cost that we would like to minimize. In this
example it is a cost. We start with the information that each mile away from the river
results in three units of cost (such as maintaining a pipeline per mile), while the distance
to the CEO's house in miles, squared, gives units of cost for his travel logistics.
In this coordinate system, the plant distance to river = x + 5, while plant distance to
CEO = -x + 5. This gives us a utility function of:
crude diagram (please ignore bad algebra)
Variable x the thing we have control over, in this case the position of the factory
along the road from -5 to 5, and the utility function u(x) represents dollars in revenue
we would like to maximize, or dollars in cost that we would like to minimize. In this
example it is a cost. We start with the information that each mile away from the river
results in three units of cost (such as maintaining a pipeline per mile), while the distance
to the CEO's house in miles, squared, gives units of cost for his travel logistics.
In this coordinate system, the plant distance to river = x + 5, while plant distance to
CEO = -x + 5. This gives us a utility function of:
- u(x) = 3*(5+x) + (5 - x)^2
- u(x) = x^2 - 7x + 40
- u'(x) = 2x - 7
 Oliver Heaviside picture
from Wikipedia commons
( en.wikipedia.org/wiki/Heaviside )
I explained that Maxwell's famous equations of electrodynamics wouldn't fit on a tee shirt
if it had't been for Oliver; we'd need a bed sheet.
Oliver Heaviside picture
from Wikipedia commons
( en.wikipedia.org/wiki/Heaviside )
I explained that Maxwell's famous equations of electrodynamics wouldn't fit on a tee shirt
if it had't been for Oliver; we'd need a bed sheet.
 Maxwell's Equations shirt from
www.zazzle.com
(Notice that insidious del operator.)
Maxwell's Equations shirt from
www.zazzle.com
(Notice that insidious del operator.)
Lesson 6 — 29 June 2010
concepts:- series of differences between squares ( betterexplained.com/articles/surprising-patterns-in-the-square-numbers-1-4-9-16 )
- Babbage's difference engine ( en.wikipedia.org/wiki/Difference_engine )
- Taylor series ( en.wikipedia.org/wiki/Taylor_series )
- ordinary differential equations (ODEs) ( en.wikipedia.org/wiki/Ordinary_differential_equations )
- 0
1
1 2
3 0
4 2
5 0
9 2
7 0
16 2
9 0
25 2
11 0
36 2
13
49
 cover illustration from "The Difference Engine"
(novel, 1991) by Gibson & Sterling
( www.amazon.com/exec/obidos/ASIN/0440423627/hip-20 )
I told her how I had a delightful physics professor at UCSC named Dorfman,
who was South African and had a clipped British-esque accent. One day he asked
us if we kenw what a Taylor Series was. We'd all studied the proof of the
Taylor Series in the prerequisite calculus classes, but nobody understood it.
He was aghast. "What are they teaching you?" he muttered. He took a 20-minute
detour and gave us a proof-less explanation of what it meant and what it
was for. And it was this intuition that I wanted to pass on to me daughter.
Consider a problem that Norbert Weiner studied a lot, when he was inventing
cybernetics, function prediction. Let's say you've got a series of
numbers coming down a pipe at regular intervals, like readings from a temperature
sensor, or stock purchse prices from the NASDDAQ. Given a series of numbers,
how do you predict the next one?
ZERO ORDER
One simple solution is to always guess zero. It's probably going to be wrong
most of the time, but it will also probably have an error that stays within
a stable range. It's also very inexpensive to compute.
FIRST ORDER
A better approximation is to guess a contstant, C, picked by some reasonable
process like the last value, or an average of previous values. It will also
probably be wrong, but have a stable error range.
SECOND ORDER
If you look at the last two values and subrtact them, and get a difference
(often called delta), and then add the delta to the last value to
apply the change again, this gives an even better guess.
HIGHER ORDERS
By taking differences of differnces and finding rates of rates of change,
etc., the order of approximation can be raised and often improved. (Of course,
for every function prediction scheme there are toxic functions that mess it up.)
If you take this descrete example and generalize it for a coninuum, you get
approximations of the form:
0: y = 0
1: y = C
2: y = Ax + C
3: y = Ax^2 Bx + C
etc.
The Taylor series expoits this almost magical ability of polynomials to
approximate continuous functions. The actual formula given by Taylor is:
cover illustration from "The Difference Engine"
(novel, 1991) by Gibson & Sterling
( www.amazon.com/exec/obidos/ASIN/0440423627/hip-20 )
I told her how I had a delightful physics professor at UCSC named Dorfman,
who was South African and had a clipped British-esque accent. One day he asked
us if we kenw what a Taylor Series was. We'd all studied the proof of the
Taylor Series in the prerequisite calculus classes, but nobody understood it.
He was aghast. "What are they teaching you?" he muttered. He took a 20-minute
detour and gave us a proof-less explanation of what it meant and what it
was for. And it was this intuition that I wanted to pass on to me daughter.
Consider a problem that Norbert Weiner studied a lot, when he was inventing
cybernetics, function prediction. Let's say you've got a series of
numbers coming down a pipe at regular intervals, like readings from a temperature
sensor, or stock purchse prices from the NASDDAQ. Given a series of numbers,
how do you predict the next one?
ZERO ORDER
One simple solution is to always guess zero. It's probably going to be wrong
most of the time, but it will also probably have an error that stays within
a stable range. It's also very inexpensive to compute.
FIRST ORDER
A better approximation is to guess a contstant, C, picked by some reasonable
process like the last value, or an average of previous values. It will also
probably be wrong, but have a stable error range.
SECOND ORDER
If you look at the last two values and subrtact them, and get a difference
(often called delta), and then add the delta to the last value to
apply the change again, this gives an even better guess.
HIGHER ORDERS
By taking differences of differnces and finding rates of rates of change,
etc., the order of approximation can be raised and often improved. (Of course,
for every function prediction scheme there are toxic functions that mess it up.)
If you take this descrete example and generalize it for a coninuum, you get
approximations of the form:
0: y = 0
1: y = C
2: y = Ax + C
3: y = Ax^2 Bx + C
etc.
The Taylor series expoits this almost magical ability of polynomials to
approximate continuous functions. The actual formula given by Taylor is:
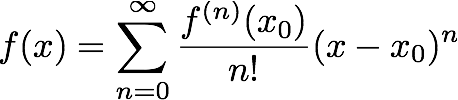 |
| IN | OUT |
|---|---|
| f(0) = 0 | f(x) = 0 |
| f'(0) = 1 | f(x) = x |
| f''(0) = 0 | f(x) = x |
| f'''(0) = -1 | f(x) = x - x^3/3 |
 |
| problem | solution |
|---|---|
| x'(t) = 0 | x(t) = C |
| x'(t) = 1 | x(t) = t + C |
| x'(t) = x | x(t) = e^t + C |
| x''''(t) = x | x(t) = sin(t + B) + C |
Lesson 7 — 31 July 2010
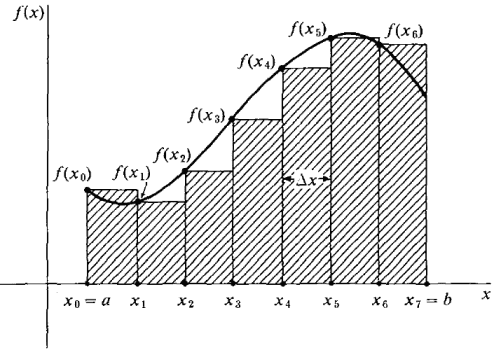
concepts:- integral ( en.wikipedia.org/wiki/Integral )
- fundamental theorem of calculus ( en.wikipedia.org/wiki/Fundamental_theorem_of_calculus )
- Newton's and Leibniz's notations ( en.wikipedia.org/wiki/Newton%27s_notation ) ( en.wikipedia.org/wiki/Leibniz%27s_notation )
-
1
2 1
3
2 4
5
2 9
7
2 16
9
2 25
11
2 36
13
2
 |
 |
 The University of Arizon math department web site has a typical version of this
classic problem, number 2A.
( math.arizona.edu/~ghystad/relatedrates.pdf )
Q: A water tank is in the shape of an inverted cone with height 20 m and top
radius 4 m. Water is flowing into the tank at a constant rate of 0.1 m3/min.
How fast is the water level in the tank rising at the moment that the depth
of the water is 5 m?
I pointed out that in the on-line document, the first 3 steps are the "word problem"
and setting up the equation. You can then let Wolfram Alpha do steps 4 and 5.
After that (or maybe before) I think we watched Mechanical Universe
Epsiode 7: "Integration" (29:08) and discussed it.
( video.google.com/videoplay?docid=7292513217416289653 )
The University of Arizon math department web site has a typical version of this
classic problem, number 2A.
( math.arizona.edu/~ghystad/relatedrates.pdf )
Q: A water tank is in the shape of an inverted cone with height 20 m and top
radius 4 m. Water is flowing into the tank at a constant rate of 0.1 m3/min.
How fast is the water level in the tank rising at the moment that the depth
of the water is 5 m?
I pointed out that in the on-line document, the first 3 steps are the "word problem"
and setting up the equation. You can then let Wolfram Alpha do steps 4 and 5.
After that (or maybe before) I think we watched Mechanical Universe
Epsiode 7: "Integration" (29:08) and discussed it.
( video.google.com/videoplay?docid=7292513217416289653 )
Lesson 8 — 2 August 2010
concepts:- deterministic finite automaton (finite state machine without inputs) ( en.wikipedia.org/wiki/Deterministic_finite_automaton )
- basin of attraction ( en.wikipedia.org/wiki/Basin_of_attraction )
- finite state machine with inputs ( en.wikipedia.org/wiki/Finite-state_machine )
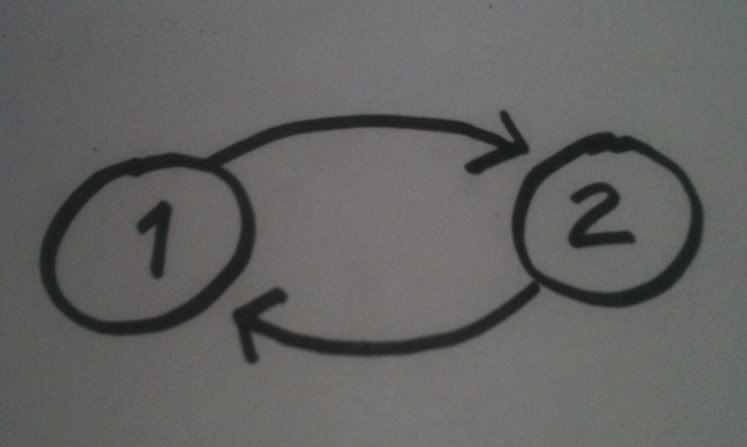 2 state FSM drawn by ABS
If we number the states 1 & 2, the output of this machine is:
1 2 1 2 1 2 1 2...
Everybody following along? Good. Things get more compicated as you add
states. Ashby defined the variety of a FSM as a measure of
the number of states it can possibly end up in, and pointed out that over
time the variety always stays the same or goes down. (Kind of like the
way entropy always stays the same or goes up.) If an arrow leads out of
state 1 to state 2, but there is no path back through the machine from
2 to 1 (i.e., the transisiton from 1 to 2 is a "trap door"), then once
the transition is made to state 2 the variety has gone down permanently.
I explained how you can sort all the states in a machine into basins of
attraction, kind of like watersheds. If you spit in San Deigo County
chances are the water will end up in one of 10 rivers or creeks (San Juan,
Santa Margarita, San Luis Rey, Carlsbad, San Dieguito, Penasquitos, San Diego,
Pueblo, Sweetwater, Otay, Tijuana), fed by the ten basins or watersheds.
2 state FSM drawn by ABS
If we number the states 1 & 2, the output of this machine is:
1 2 1 2 1 2 1 2...
Everybody following along? Good. Things get more compicated as you add
states. Ashby defined the variety of a FSM as a measure of
the number of states it can possibly end up in, and pointed out that over
time the variety always stays the same or goes down. (Kind of like the
way entropy always stays the same or goes up.) If an arrow leads out of
state 1 to state 2, but there is no path back through the machine from
2 to 1 (i.e., the transisiton from 1 to 2 is a "trap door"), then once
the transition is made to state 2 the variety has gone down permanently.
I explained how you can sort all the states in a machine into basins of
attraction, kind of like watersheds. If you spit in San Deigo County
chances are the water will end up in one of 10 rivers or creeks (San Juan,
Santa Margarita, San Luis Rey, Carlsbad, San Dieguito, Penasquitos, San Diego,
Pueblo, Sweetwater, Otay, Tijuana), fed by the ten basins or watersheds.
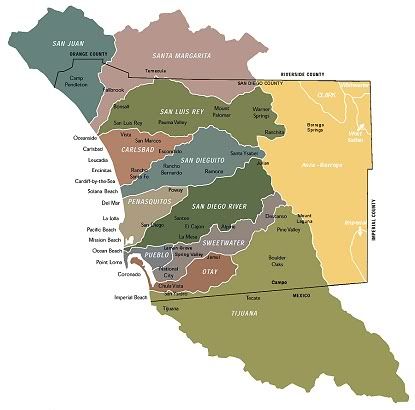 San Diego County watersheds from county web site
www.sdcounty.ca.gov/pds/watershed/watersheds.html
Next I explained a finite state machine with inputs, in which each
transition is controlled by an input message, and the machine can be expressed
by a table listing each possible input vs. each state, giving the new state.
For example, consider this simplistic text-based Adventure Game:
San Diego County watersheds from county web site
www.sdcounty.ca.gov/pds/watershed/watersheds.html
Next I explained a finite state machine with inputs, in which each
transition is controlled by an input message, and the machine can be expressed
by a table listing each possible input vs. each state, giving the new state.
For example, consider this simplistic text-based Adventure Game:
| input -> initial state | V | OUT | IN | UP | DOWN | NORTH | SOUTH |
|---|---|---|---|---|---|---|
| well house | outside well house | well house * | well house * | secret basement | well house * | outside well house |
| secret basement | secret basement * | well house | secret basement * | secret basement * | secret basement * | secret basement * |
| outside well house | outside well house * | well house | outside well house * | down hill | well house | down hill |
| down hill | down hill * | down hill * | outside well house | lost in woods | outside well house | lost in woods |
| lost in woods | lost in woods * | lost in woods * | lost in woods * | lost in woods * | lost in woods * | lost in woods * |
| input -> initial state | V | OUT | IN | UP | DOWN | NORTH | SOUTH |
|---|---|---|---|---|---|---|
| dungeon | dungeon * | dungeon * | dungeon * | dungeon * | dungeon * | dungeon * |
Lesson 9 — 6 August 2010
concepts:- Law of Requisite Variety ( en.wikipedia.org/wiki/Law_of_Requisite_Variety )
- attractor ( en.wikipedia.org/wiki/Attractor )
- dynamics ( en.wikipedia.org/wiki/Analytical_dynamics )
The revolution that Newton introduced into science had three independent components. Two belonged to physics: the inverse-square law of gravitation and the idea that force is proportional to acceleration. The third, and most basic, was mathematical: the calculus, as the language in which all dynamics is to be formulated. The essence of the calculus lies in the concept of a differential equation as the basic form of explanation of physical change. A differential equation gives the rule by which the state of the system determines the changes of state of the system, which then determine its future evolution.Lastly I showed her some interactive 3D visualizations I have done of systems of 2D and 3D ODEs. Some of these appear in static picture form on my web site: ( www.well.com/user/abs/math_rec.html ) The systems including an arms race by 2 nations as modeled by Lewis Fry Richardson, and Edward Lorenz's first chaotic attractor, found in an oversimplified convection current airflow model.
 Lorenz attractor viz by ABS
Some YouTube videos now online give a flavor of these interactive visualizations.
( www.google.com/search?tbm=vid&hl=en&q=lorenz+attractor )
I don't think we watched Mechanical Universe Epsiode 9: "Moving In
Circles" (28:51), but we might have.
( video.google.com/videoplay?docid=268446297904859913 )
Lorenz attractor viz by ABS
Some YouTube videos now online give a flavor of these interactive visualizations.
( www.google.com/search?tbm=vid&hl=en&q=lorenz+attractor )
I don't think we watched Mechanical Universe Epsiode 9: "Moving In
Circles" (28:51), but we might have.
( video.google.com/videoplay?docid=268446297904859913 )
Lesson 10 — 10 August 2010
concepts:- simple harmonic oscillator ( en.wikipedia.org/wiki/Simple_harmonic_motion )
- phase plot ( en.wikipedia.org/wiki/Phase_space )
 I decided I needed to back-fill on the concept of state space
and the related concept of a phase plot.
So I read from Ralph Abraham and C. D. Shaw's so-called "chaos comix," Dynamics,
the Geometry of Behavior (1992), from book 1, pp. 1.1 - 2.4.7, which begins:
I decided I needed to back-fill on the concept of state space
and the related concept of a phase plot.
So I read from Ralph Abraham and C. D. Shaw's so-called "chaos comix," Dynamics,
the Geometry of Behavior (1992), from book 1, pp. 1.1 - 2.4.7, which begins:
1.1 STATE SPACEI wish I could lay my hands on one of the two four-volume sets that I own, but they're in storage. I suppose I'll quote it some other time. Meanwhile, to keep up with Abraham, check his web site at the Visual Math Institute. ( www.vismath.org I went on to explain how Ordinary Differential Equations (ODEs) are sorted out. A single equation with one "variable" (actually a function) x(t) will define the derivative of x(t) in terms of some function f of x. If f is linear then the equation is in principle solvable, and the solution will be another function s(t). x' = f(x) A pair of ODEs can have two "variables," x(t) and y(t), and two equations defining the two derivatives in terms of two functions f and g of x and y. Again, if f and g are linear then the set of equations tends to be solvable. x' = f(x, y) y' = g(x, y) You will sometimes see higher order derivatives, like the second derivative of y set to x, while the first derivative of x is some function of x and y. y'' = x x' = f(x, y) Or you may even see polynomial-like equations in which derivatives of different orders have constant factors (shown here in caps) which can be easily put into matrix form, allowing all sorts of tricks. A y''' + B y'' + C y + D = 0 As always, here in the 21sty century the main issue is getting the equations right, and then letting the computers solve them if possible or simulate them if not. I showed how to solve a simple physics problem with these tools: the linear spring. This is kind of like the bowling ball hanging from a slinkey (or what ever it was) in the Periodic Motions film. Imagine that a spring provides force in the opposite direction of its displacement with spring constant k, and it is attached to mass m. We have the force on the spring as: f = -kx and Newton's law: f = ma By algebra: ma = -kx a = -kx/m x'' = -kx/m (Note that x'' is another name for a, acceleration.) Setting k and m to 1 for simplicity, and plugging this result into Wolfram Alpha, x'' = -x ( www.wolframalpha.com/input/?i=x%27%27+%3D+-x ) Note that we get an equation, a graph, and a phase plot back.
Lesson 11 — 17 August 2010
concepts:- Markov machine ( en.wikipedia.org/wiki/GNFA )
- Markov tree ( en.wikipedia.org/wiki/Markov_chain )
- gradient state-space ( en.wikipedia.org/wiki/Gradient )
 Markov machine from "Computer
simulation of the activity of the elderly person
living independently in a Health Smart Home"
www.sciencedirect.com/science/article/pii/S0169260712001782
A Markov machine with inputs bases the probabilites on the state it is
in and the input it receives.
A technique developed by Dr. Markov is the Markov tree or chain.
You simply draw a tree of all possible outcomes after a certain number of steps,
and label each branch with the probablity of that transition. To find the probablity
of a "leaf" on the tree, start at the root and multiply probabilities.
Markov machine from "Computer
simulation of the activity of the elderly person
living independently in a Health Smart Home"
www.sciencedirect.com/science/article/pii/S0169260712001782
A Markov machine with inputs bases the probabilites on the state it is
in and the input it receives.
A technique developed by Dr. Markov is the Markov tree or chain.
You simply draw a tree of all possible outcomes after a certain number of steps,
and label each branch with the probablity of that transition. To find the probablity
of a "leaf" on the tree, start at the root and multiply probabilities.
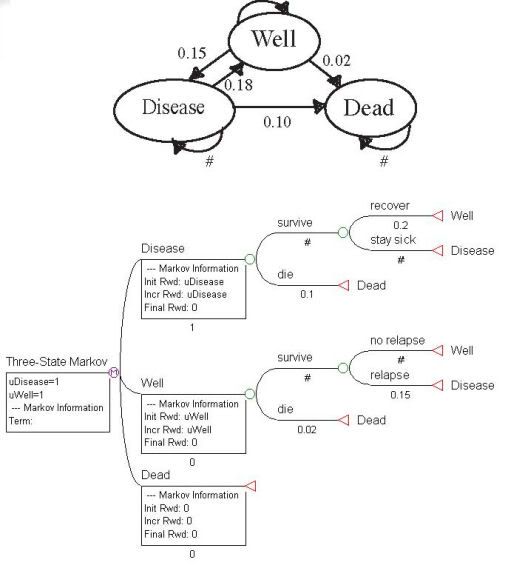 Markov machine and tree tree from "Markov Models -
State Transition Models" by TreeAge Software
www.treeage.com/learnMore/MarkovModels.html
Next I trotted out the old "Monty Hall Problem" which causes so much confusion
and arguing. The Wikipedia article explains it with a Markov tree.
( en.wikipedia.org/wiki/Monty_Hall_problem )
Then I read some more from Abraham [1992] (op cit.) about gradient spaces,
then from my blog on Eigenvectors (op. cit.), abd pages 2-3 of Garfinkel [1983] (op. cit.).
I also wanted to show daughter some more detail of the interactive visualization
of the Lorenz Attractor and other state spaces. I'd use the AVS5 software from
AVS Inc., and written a "plug-in" I called simply "system" in the C language.
I showed how I could make a change to the 3 ODEs in the code, defining variables
"x_dot," "y_dot" and "z_dot" in terms of x, y, z, and some constants on knobs.
Then I re-ran the visualization showing the change.
Winding up, I reviewed our list of goals from the first lesson and declared victory.
I closed with a look at the table from Bertalanffy's "General Systems Theory" (1968)
on the difficulty of solving equations.
( www.well.com/user/abs/equations.html )
This is the "dirty little secret" of Newton's scientific revolution: in most cases
we can write the equations but not solve them! For four hundred years there was
practically a cover-up, until cheap computers and simulation came along to save us.
Markov machine and tree tree from "Markov Models -
State Transition Models" by TreeAge Software
www.treeage.com/learnMore/MarkovModels.html
Next I trotted out the old "Monty Hall Problem" which causes so much confusion
and arguing. The Wikipedia article explains it with a Markov tree.
( en.wikipedia.org/wiki/Monty_Hall_problem )
Then I read some more from Abraham [1992] (op cit.) about gradient spaces,
then from my blog on Eigenvectors (op. cit.), abd pages 2-3 of Garfinkel [1983] (op. cit.).
I also wanted to show daughter some more detail of the interactive visualization
of the Lorenz Attractor and other state spaces. I'd use the AVS5 software from
AVS Inc., and written a "plug-in" I called simply "system" in the C language.
I showed how I could make a change to the 3 ODEs in the code, defining variables
"x_dot," "y_dot" and "z_dot" in terms of x, y, z, and some constants on knobs.
Then I re-ran the visualization showing the change.
Winding up, I reviewed our list of goals from the first lesson and declared victory.
I closed with a look at the table from Bertalanffy's "General Systems Theory" (1968)
on the difficulty of solving equations.
( www.well.com/user/abs/equations.html )
This is the "dirty little secret" of Newton's scientific revolution: in most cases
we can write the equations but not solve them! For four hundred years there was
practically a cover-up, until cheap computers and simulation came along to save us.
Postscript
 Just got The Manga Guide to Linear Algebra (2012) today.
( www.amazon.com/exec/obidos/ASIN/1593274130/hip-20 )
I can hardly wait to read it. I'm pretty sure I would've used it for the calculus
class if it had been available then...
Just got The Manga Guide to Linear Algebra (2012) today.
( www.amazon.com/exec/obidos/ASIN/1593274130/hip-20 )
I can hardly wait to read it. I'm pretty sure I would've used it for the calculus
class if it had been available then...
Note Re:
"If It's Just a Virtual Actor, Then Why Am I Feeling Real Emotions?"
 Part five of this serialization will appear next time.
Part five of this serialization will appear next time.