3D Models of Geodesics

by Alan B. Scrivener

geodesic dome over south pole

geodesic dome at Expo '67, Montreal

geodesic dome "Spaceship Earth" at EPCOT, Walt Disney Wolrd, Florida

geodesic dome playground equipment

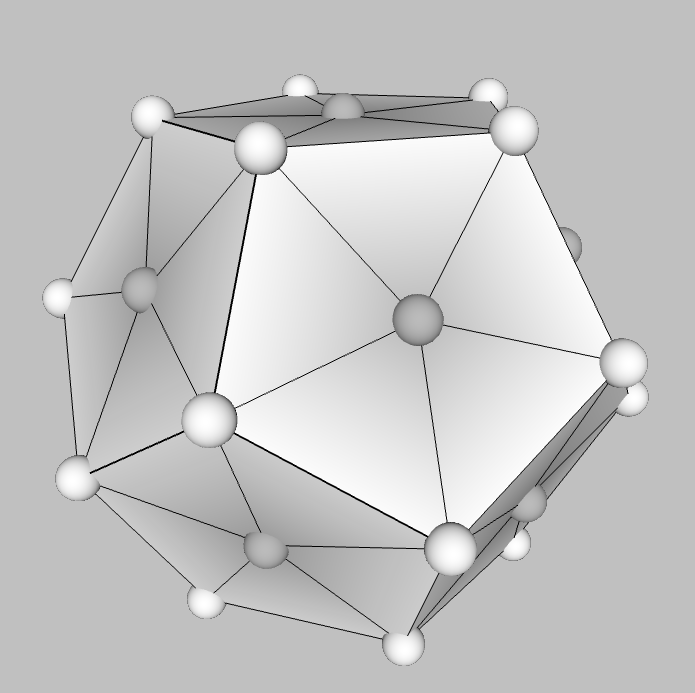
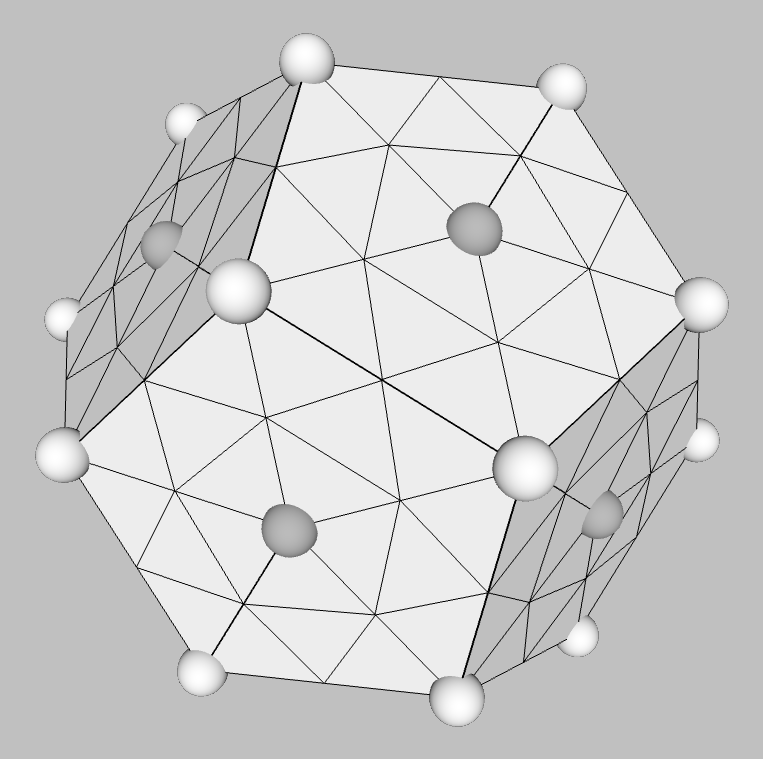
"An icosahedron and related symmetry polyhedra can be used to define a high geodesic polyhedron by dividing triangular faces into smaller triangles, and projecting all the new vertices onto a sphere. Higher order polygonal faces can be divided into triangles by adding new vertices centered on each face. The new faces on the sphere are not equilateral triangles, but they are approximately equal edge length."

— Wikipedia article on Geodesic polyhedron

How to Make a Geodesic Polyhedron

Start with a polyhedron.	Triangulate all polygons having more than 3 sides by adding a central point (if needed).	Pick a frequency f > 1. Divide each edge into f segments by adding points; add interior points as needed. Turn each original triangle into a mesh of f2 triangles.	"Puff" the shape out to a set of points on a unit sphere, by moving each point towards or away from the origin until its distance from the origin is one.

Interactive 3D Models

Click an image to open an interactive 3D app.

seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
tetrahedron four faces (triangles) one of the five Platonic Solids dual of itself space filling with the octahedron nicknames: triangle-base pyramid, D-4 Dungeons and Dragons (D&D) dice type D-4				tetAGeod4.html	tetVGeod5.html no facets, lines, spheres, no puff tetVPGeod5.html no facets, lines, spheres, puff tetWGeod5.html white facets, lines, spheres, no puff tetWPGeod5.html white facets, lines, spheres, puff tetCGeod5.html color facets, lines, spheres, no puff tetCPGeod5.html color facets, lines, spheres, puff
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
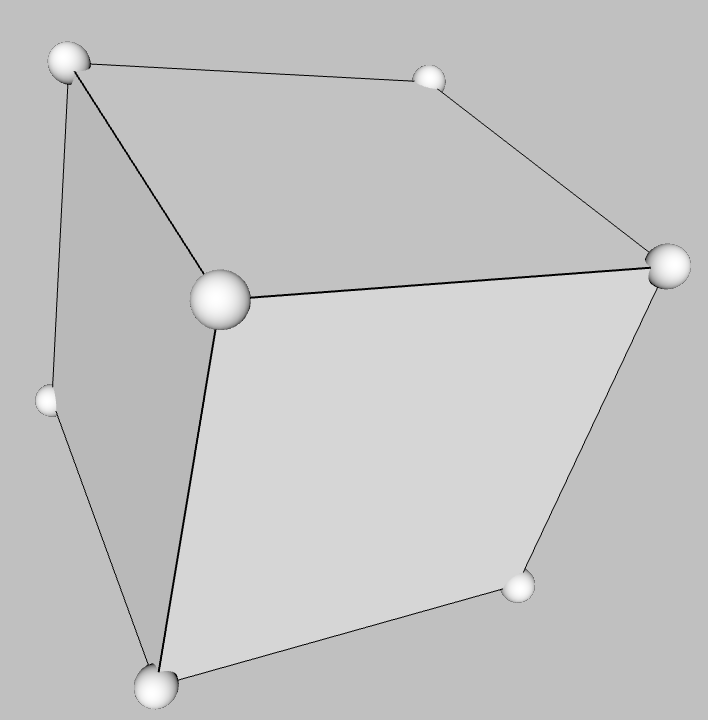
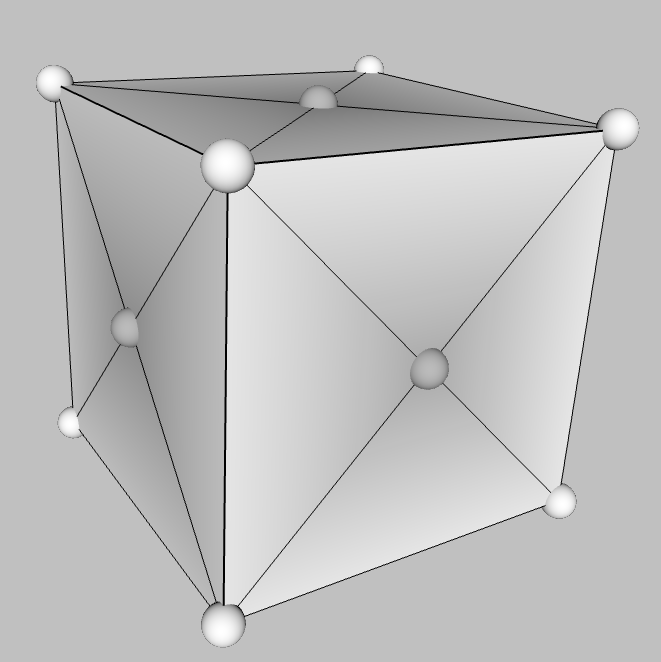
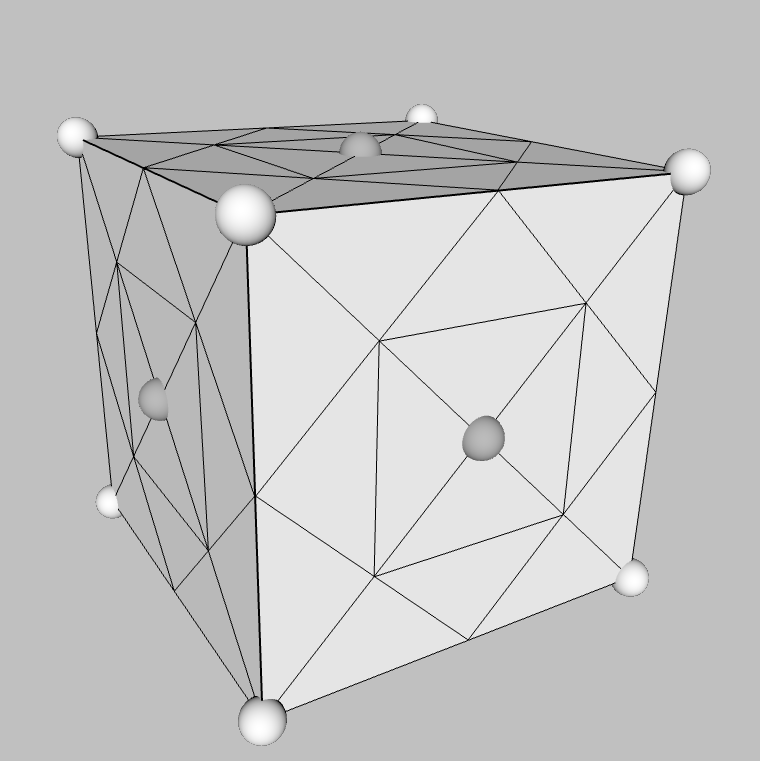
cube six faces (squares) one of the five Platonic Solids dual of the octahedron space filling nicknames: hexahedron, D-6 Note: each square is split into four triangles, making twenty-four triangular faces.	cube_rawV.html raw seed, no facets, lines, spheres cubeV.html triangulated seed, no facets, lines, spheres cube_raw.html raw seed, white facets, lines, spheres cube.html triangulated seed, white facets, lines, spheres	cubeVGeod2.html no facets, lines, spheres, no puff cubeVPGeod2.html no facets, lines, spheres, puff cubeWGeod2.html white facets, lines, spheres, no puff cubeWPGeod2.html white facets, lines, spheres, puff cubeCGeod2.html color facets, lines, spheres, no puff cubeCPGeod2.html color facets, lines, spheres, puff		cubeAGeod4.html
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
octahedron eight faces (triangles) one of the five Platonic Solids dual of the cube space filling with the tetrahedron nicknames: pyramid on a mirror, D-8
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
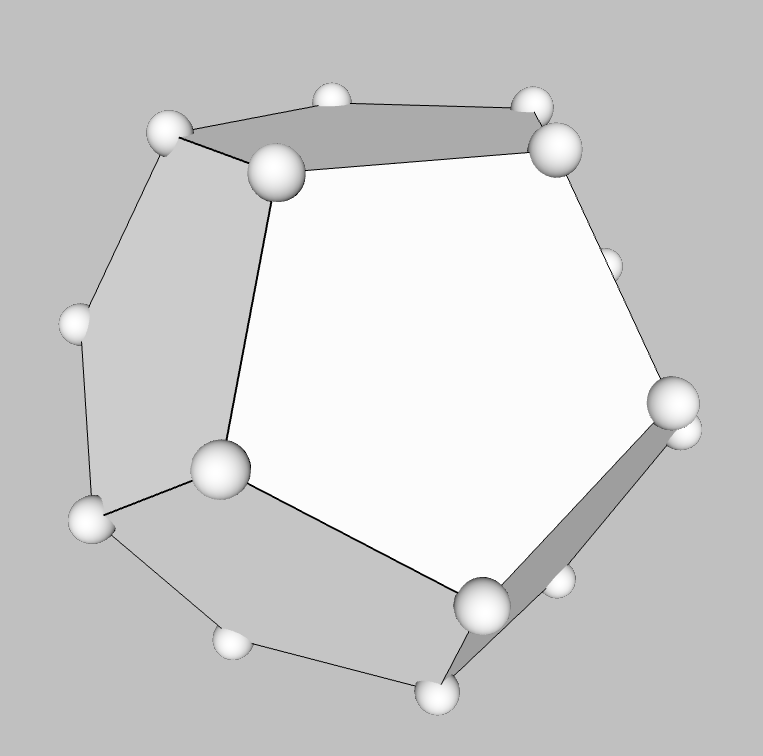
dodecahedron twelve faces (pentagons) one of the five Platonic Solids dual of the icosahedron nicknames: D-12 Note: each pentagon is split into five triangles, making sixty triangular faces.		dodecVGeod2.html no facets, lines, spheres, no puff dodecVPGeod2.html no facets, lines, spheres, puff dodecWGeod2.html white facets, lines, spheres, no puff dodecWPGeod2.html white facets, lines, spheres, puff dodecCGeod2.html color facets, lines, spheres, no puff dodecCPGeod2.html color facets, lines, spheres, puff		dodecAGeod4.html
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
icosahedron twenty faces (triangles) one of the five Platonic Solids dual of the dodecahedron nicknames: D-20		icosVGeod2.html no facets, lines, spheres, no puff icosWGeod2.html white facets, lines, spheres, no puff icosCGeod2.html color facets, lines, spheres, no puff			icosAGeod5.html	icosVGeod10.html no facets, lines, spheres, no puff icosVPGeod10.html no facets, lines, spheres, puff icosWGeod10.html white facets, lines, spheres, no puff icosWPGeod10.html white facets, lines, spheres, puff icosCGeod10.html color facets, lines, spheres, no puff icosCPGeod10.html color facets, lines, spheres, puff
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
snub cube 38 faces (32 triangles, 6 squares) one of the thirteen Archimedean Solids dual of the pentagonal icositetrahedron nicknames: snic	snubc_rawV.html raw seed, no facets, lines, spheres snubcV.html triangulated seed, no facets, lines, spheres snubc_raw.html raw seed, white facets, lines, spheres snubc.html triangulated seed, white facets, lines, spheres	snubcVGeod2.html no facets, lines, spheres, no puff snubcVPGeod2.html no facets, lines, spheres, puff snubcWGeod2.html white facets, lines, spheres, no puff snubcWPGeod2.html white facets, lines, spheres, puff snubcCGeod2.html color facets, lines, spheres, no puff snubcCPGeod2.html color facets, lines, spheres, puff		snubcAGeod4.html
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
rhombic dodecahedron twelve faces (rhombuses formed from two triangles) one of the thirteen Catalan Solids dual of the cuboctahedron space filling Note: each rhombus is split into two triangles, making twenty-four triangular faces.	rhombic_rawV.html raw seed, no facets, lines, spheres rhombicV.html triangulated seed, no facets, lines, spheres rhombic_raw.html raw seed, white facets, lines, spheres rhombic.html triangulated seed, white facets, lines, spheres	rhombicVGeod2.html no facets, lines, spheres, no puff rhombicVPGeod2.html no facets, lines, spheres, puff rhombicWGeod2.html white facets, lines, spheres, no puff rhombicWPGeod2.html white facets, lines, spheres, puff rhombicCGeod2.html color facets, lines, spheres, no puff rhombicCPGeod2.html color facets, lines, spheres, puff	rhombicAGeod3.html		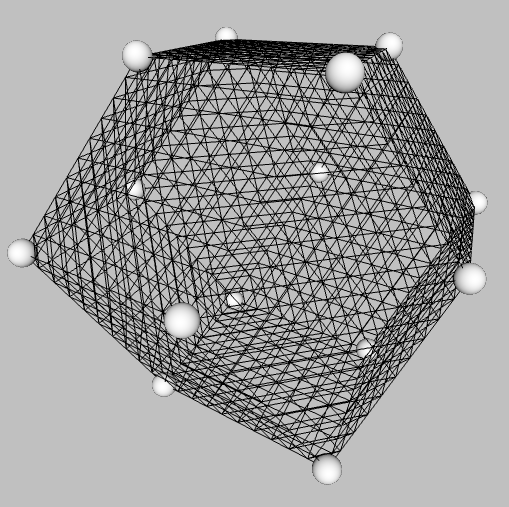	rhombicVGeod10.html no facets, lines, spheres, no puff rhombicWGeod10.html white facets, lines, spheres, no puff
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq
cuboctahedron 14 faces (8 triangles, 6 squares) dual of the rhombic dodecahedron nicknames: jitterbug, Vector Equilibrium (R.B. Fuller)	cuboct_rawV.html raw seed, no facets, lines, spheres cuboctV.html triangulated seed, no facets, lines, spheres cuboct_raw.html raw seed, white facets, lines, spheres cuboct.html triangulated seed, white facets, lines, spheres	cuboctAGeod2.html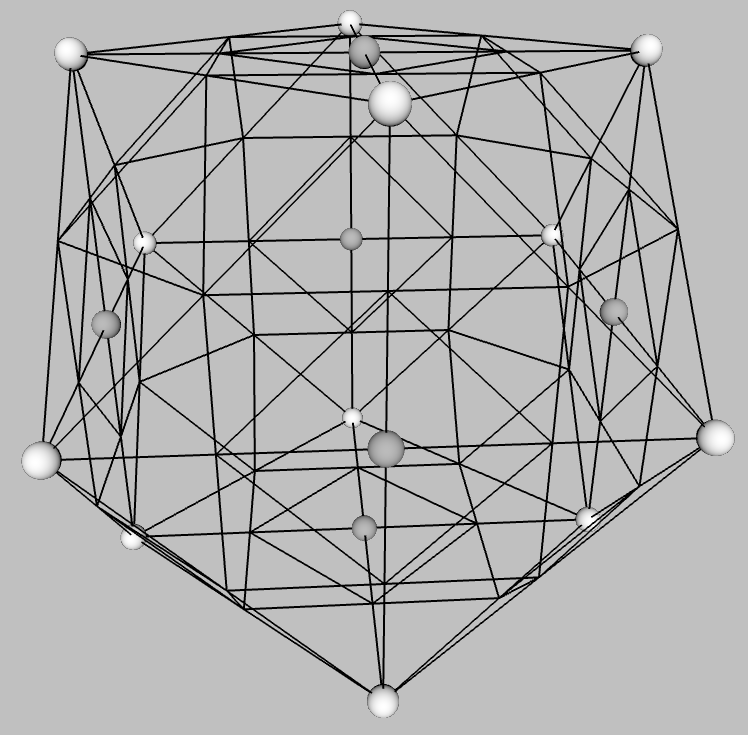 cuboctVGeod2.html no facets, lines, spheres, no puff cuboctCGeod2.html color facets, lines, spheres, no puff				cuboctVGeod10.html no facets, lines, spheres, no puff cuboctCGeod10.html color facets, lines, spheres, no puff
seed name	seed (1-freq)	2-freq	3-freq	4-freq	5-freq	10-freq

filename taxonomy:
    [mode][seed][options]Geod[f]
mode:
    Run   production mode
    Test  debug writes, comnpare to good output
seed:
    Cube [6 tri]
    Cuboct
    Dodec [12 pen]
    Icos [20 tri]
    Oct [8 tri]
    Rhombic [12 rho]
    Tet [4 tri]
options:
    N - no spheres (default = yes spheres)
    V - vectors only (all have vectors)
    W - white faces
    C - color faces
    F - flat facets
    P - "puffed" facets