The ECCO System
Cybernetic Principles for Effective Control in Complex Organizations
Click here for footnotes, Ch.4.
CHAPTER IV
Cybernetics and the Control of Complex Systems
The term "cybernetics" was coined by mathematician Norbert Wiener in the 1940s. He derived the term from kubernetes, the Greek word for "steersman", which is also the root of our word "governor". His original interest was in the theory of messages to control machinery, particularly automated devices like guided missiles. He was fascinated with the notion of a general theory of control based on information feedback, not only of machines, but of neurological systems of both humans and animals. Wiener's original definition was that cybernetics was "the study of communication and control in the animal and the machine." 1
Over the next several years, the term cybernetics came to be associated with the study of a variety of circular causal processes, including those governing dynamically stable ecosystems, as well as the dynamics underlying stabilities of cultures, and of organizations and societies. Cybernetics has come to be understood as the study of the behavior of goal seeking systems as well as systems which behave as if they had goals. William Ross Ashby, a leading cybernetic theorist in the 1950s and 60s, wrote An Introduction to Cybernetics where he discusses principles of the field:
Co-ordination, regulation, and control will be [the book's] themes, for these are of the greatest biological and practical interests. . . . Cybernetics . . . is a 'theory of machines', but it treats not things but ways of behaving. . . .
One [advantage] is that it offers a single vocabulary and a single set of concepts suitable for representing the most diverse types of systems. . . . And it can provide the common language by which discoveries in one branch can readily be made use of in the others. . . .
[Another is] that it offers a method for the scientific treatment of the system in which complexity is outstanding and too important to be ignored. . . .
Cybernetics offers the hope of providing effective methods for the study, and control, of systems that are intrinsically extremely complex."2
Ashby also saw the need to provide a formal language for cybernetics, so important concepts could be expressed clearly, precisely, and in a most general form. He formulated concepts of dynamic systems, previously described in terms of differential equations, in terms of Bourbaki set theory. This allowed the description of dynamic systems as state transition systems to be specified using state transition matrices. This allowed a variety of qualitative as well as quantitative variables to be expressed unambiguously. He also introduced the formalisms of Claude Shannon's Information Theory in order to quantify concepts of communication and regulation. Finally, he used diagrams of immediate effects to show graphically the influences of various system parts on each other.
Basic Principles of Regulation and Control
In cybernetics, all instances of control depend on feedback--some circular causal processes, where two elements are related in such a way that the state of each has an effect on the other. This includes the more specialized case, where feedback is limited to specific data which will be analyzed, compared to a desired goal state, and serve as a guide for corrective action. In all cases, it will be noted, that the most efficient feedback (that which maintains a nearly stable value around a goal value) for error controlled mechanisms and for the development of successful behaviors in adaptive mechanisms is "short-loop" feedback. The longer it takes for information (or physical effect) to be received and processed (correctively or adaptively), the less efficient the control or adaptation process is likely to be.3 In addition, it is axiomatic that the quality of the feedback, in terms of appropriate level of detail, and measurement of parameters closely related to the condition of that which is to be controlled, is directly related to the potential effectiveness of the regulatory system.
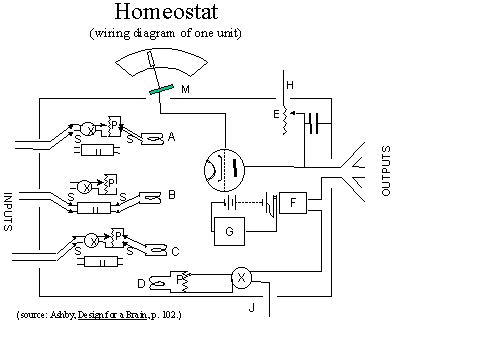
Simple, designed error control devices such as thermostats have a fixed structure. Although the desired goal state (temperature) may be reset, the structure of the mechanism by which this is accomplished is fixed. The device has built-in restrictions on its capabilities. Ashby was interested in the mechanisms for adaptivity in control systems. To demonstrate some important principles of adaptivity, he constructed an electro-mechanical device called a Homeostat.
Flexible Control: The Homeostat
Ashby's homeostat4 contained no teleological element and no fixed error-control mechanism, yet it behaved "adaptively" in many important respects. Since this mechanism is of central importance to understanding a number of cybernetic concepts, it will be worth describing here in some detail. (The homeostat had a number of interesting and important properties and details of construction. Only those relevant to the present discussion will be discussed here. For a more complete discussion of the homeostat, see Ashby's Design for a Brain, 1960)
The original homeostat consisted of four identical units, supplied with DC current, and connected so that the input for each unit consisted of the output from the other three. Each input to each unit was modified by a commutator and a potentiometer which controlled the polarity and strength of the incoming signal respectively. The amount of current reaching each unit was measured by an indicator needle whose stable (or preferred) position was a narrow zone near the center of the dial. The output of each unit was proportional to the distance of the indicator needle from the center position. When the needles of a unit were centered, the current values of the potentiometer/commutator remained unchanging. When the needle diverged from its central position, a relay was closed which energized a mechanism to randomly assign, at 3-second intervals, new values to each of the potentiometer/commutator elements of the unit until the needle returned to its central position. (See figure 1)

Figure 1
The homeostat would be started at some position away from equilibrium for one or more of the units, and would proceed to "seek" a combination of values which would typically yield the position of stability, where all of the units needles were centered. The major contributions of the homeostat were 1) the demonstration of "adaptive response" in a machine, as a consequence of the machine's configuration; 2) as a model for heterarchical (mutual) control, in the absence of external control or designed error-control mechanisms; and 3) what Aulin has called the Principle of Variable Structure,5 since the variety of parameter configurations enables a number of parameter value solutions to emerge, increasing the possibility of successful achievement of stability. Where the simple error control device has a fixed structure, the homeostat has a fixed meta-structure, and a variable internal structure. We will draw on these principles later in the chapter.
Fundamentals of Regulation
Ashby was primarily concerned with regulation, its improvement and its amplification. In Ashby's terms, regulation can be considered the selection of acts or elements from a well-defined set, which will produce a specific outcome. The "goal" is to maintain the "essential variables" of the outcome within specific limits required for survival or success. In the general case, the regulator "selects" acts to nullify the effects of a "disturbance" which threatens to drive variables out of range. A disturbance may be in the nature of a physical perturbation: a cold draft across the skin of an animal, which then selects some physiological means of compensating for loss of body heat.
Ashby describes the task of design in terms of the selection of parts, attributes or actions which will produce a product which meets a variety of goal requirements. In the case of design, the "disturbance" can be seen as simply each design choice which must be made. If the regulator knows what act to take or what element to select which will produce an outcome or product which fully meets the design requirements, the act of regulation has succeeded.
Ashby conceives of the regulation process as consisting of a set of disturbances D, which will affect the state of the entity to be controlled E. The controller C sets the values which are acceptable in E (determines the parameters of E's "essential variables"). Note that the controller may be a teleological entity, or simply a representation of the values to which a regulator must respond. The regulator R has certain regulatory actions it may take in response to the value of D, in order to keep E's essential variables within range. The relation between the disturbance D and the regulatory action of R is given in table T. If R chooses an action which corresponds to and nullifies the disturbance D, E is unaffected by the disturbance.
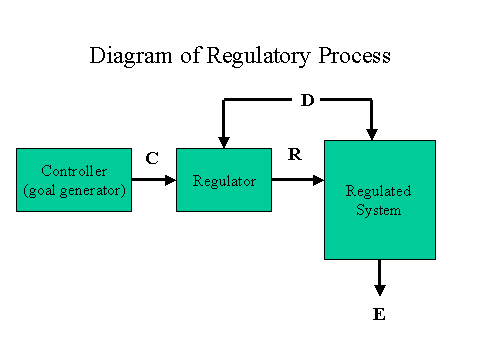
Figure 2
Consider T in the form of a table, listing D's possible values (as a choice of rows) and R's possible values (as a choice of columns). The table T might look like this:
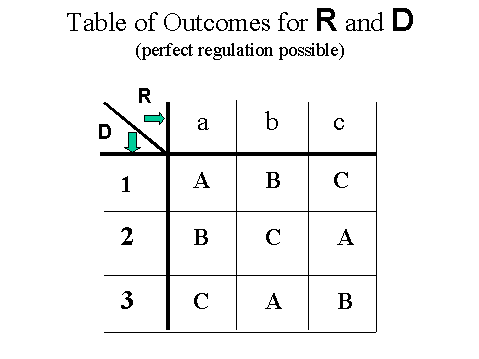
Figure 3
In this case, we can see that perfect regulation is possible. Suppose we wish to maintain an outcome of "C". If D=1 then R chooses c. If D=2, R chooses b; If D=3, then R chooses a. The same sorts of moves will be possible if R is controlling for an outcome of "A" or "B" as well.6
Let us consider a table T where D's variety is greater than R's variety:
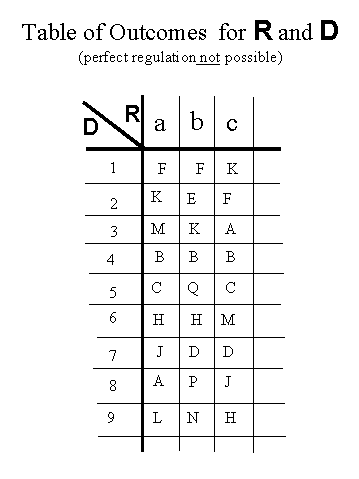
(source: W. Ross Ashby "Variety, Constraint, and the Law of Requisite Variety", in Walter Buckley, ed., Modern Systems Research for the Behavioral Scientist (Chicago: Aldine, 1968) p. 134.)
Figure 4
In this case, R cannot have complete control of the outcome. The best that R can do, in terms of keeping the variety of the outcome minimized, is given by: variety of D/variety of R; in this case 9/3 or 3 different outcomes. In many versions of the table, R will not be able to do this well, but in any version of the table, this is the best R can do.
In quantifying the variety, or uncertainty, of the outcome, i.e. the limits of regulation, Ashby uses the Claude Shannon's concept of informational entropy, H. H represents the degree of uncertainty (lack of control) of the outcome of a series of regulatory acts. H=0 indicates no uncertainty, or the possibility of perfect control. 7
Overcoming Limitations on Regulatory Effectiveness
Thus, there are at least two limitations which govern the possible effectiveness of a regulator. The first is the "Law of Requisite Variety", which states that, for perfect regulation to be possible, the regulator must have at least as much variety in regulatory actions as the variety of potential disturbances.8 The second is stated in Ashby and formalized by Aulin.9 The regulator is also limited by his ignorance of the effect that a particular regulatory act will have on the state of the outcome, given a disturbance. This is the case where the relationships between the regulator's choices R and their effects with respect to various values of D is not completely known.
Given these limits on regulatory capabilities, Ashby considered the problem of how regulation could be improved, and, later how it could be amplified. Aulin formalized the problem as follows:
If A is a variable of any kind, then H(A) is a measure of its variety. (df) . . . If A and B are two variables, the degree of their mutual dependence is measured by the entropy difference:
H(A)-HB(A)=H(B)-HA(B) =I(A,B)
If I(A,B)is zero . . . A and B are entirely independent of each other. If the conditional entropy HB(A), i.e. the average entropy of A for constant values of B, is zero, then the variable A is a function of the variable B:
HB(A)=0 <=> A = f(B)
If HA(B) too is zero, the function f is one-to-one. . . .A zero variety H(A) means that all the appearances of A are identical. A zero-conditional variety HB(A) states that for a constant B all the appearances of A are the same." 10
Continuing to trace Aulin's argument, assuming that only the dependence I(D,R) matters in the regulatory process (i.e. there are no significant interdependencies independent of the regulatory relationships among the variables), and letting the outcome variable be represented by Y, we can see that without regulation, HR(Y)=HR(D)-K (a small constant). Thus, with regulation:
H(Y) > H(D) + HD(R) - H(R) - K
That is, the variety (entropy) of the outcome depends on the variety of D, the variety of R, and the "uncertainty expressed by the conditional entropy HD(R) [which] represents the ignorance of the regulator about how to react correctly to each appearance of the disturbance D."11
Aulin goes on to conclude that:
"[O]nly a regulator that knows how to use available regulatory acts in an optimal way will reach the optimal result of regulation, which is: Hmin(Y)=H(D)-H(R)-K.
"In the general case the result of regulation . . . will be H(Y)=H(D)-Heff(R)-K,
where the effective regulatory ability Heff(R)=H(R) - HD(R) (Def.) now appears."12
Aulin suggests that the problem might be solved by a hierarchical arrangement of governors over the regulators, which have "wisdom" lacking in the first line regulators themselves. He thus proposes the general argument for the Law of Requisite Hierarchy:
"The weaker in average are the regulatory abilities and the larger the uncertainties of available regulators, the more hierarchy is needed in the organization of regulation and control to attain the same amount of regulation, if possible at all."13
Aulin developed his notion of Requisite Hierarchy, and an extensive mathematical model to explore the apparent necessity and usefulness of social hierarchy in the development of nations and societies. He shows persuasive evidence that as the "productive forces" become "self steering," i.e. their regulatory capabilities increase, the need for hierarchy correspondingly diminishes, as should the number of layers of hierarchy. If too much or too little hierarchy is present, it will, Aulin argues, have disastrous results on the peace and productive capabilities of the society.14
Aulin represents the structure of this hierarchy graphically as shown in figure 5 below.
Figure 5
The purpose of this hierarchy is the reduction of uncertainty of the outcome (increase in regulatory power) due to 1) lack of requisite variety on the part of first-line regulators R; and 2) ignorance on the part of the regulator of the effects of its acts in response to disturbance. He goes on to state that "[o]nly a regulator that knows how to use available regulatory acts in an optimal way will reach the optimal result of regulation"15 It shall be argued here that the first requirement ought to be remedied fairly simply, and the second, which has to do with co-ordination of knowledge, cannot be efficiently remedied with hierarchy at all. In fact, given certain distributions of ignorance, there is nothing to prevent, and much to recommend, a non-hierarchical solution to this problem. Ashby himself hints at such a solution.16
Two observations follow from the above discussion: 1) Maximizing the regulatory abilities (regulatory variety) of the first line regulators and 2) reducing the uncertainties associated with regulatory acts [the opacity of T] will both improve regulation and reduce the required hierarchy.
Aulin has developed his Law of Requisite Hierarchy to examine the conditions justifying social hierarchy in productive society, to the extent that it is intended to improve the survival and welfare of the society as a whole, and under what conditions that hierarchy might, or ought to, disappear. It will be useful to use his work to examine the conditions for improvement of control of outcomes in a productive enterprise, specifically the control of work processes and the control of design processes. This task may begin by examining the underlying assumptions of the necessity of hierarchy of governors Aulin proposes. There are two aspects which might be challenged: First, the justification for governors; and second, the sequential nature of the regulation.
Governors, in Aulin's plan, provide wisdom (about the ultimate effect of regulatory choices on outcome) not possessed by the individual regulators so governed. Suppose for a moment that the requisite variety of knowledge is present: The regulators together have requisite variety for governing specific assigned portions of the system locally, but do not have the wisdom to know how their regulatory acts will affect other parts of the system. Requisite variety at this level is simply a result of training and assignment of responsibility/authority. This condition may or may not obtain in so-called primitive societies with underdeveloped production forces, which Aulin wishes to address. It may have applied to conditions occurring in factories around the turn of the century, when the Weber/Taylor hierarchy was developed as the pinnacle of management science.
Let us look at a particular set of conditions on the distribution of knowledge and ignorance with respect to the Law of Requisite hierarchy, which will later be related specifically to the present manufacturing environment in terms of regulation, hierarchy and control.
Effects of Configurations of Regulatory Mechanisms
First, consider the case where, like Aulin's, a number of regulators are set up in series. The result of one regulator's action provides the input, which shall here be characterized as the initial state of Y or E or both, for the operations of the next regulator. Here, E is at least a one-dimensional vector.
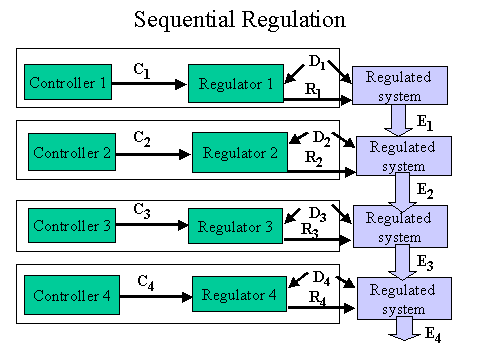
Figure 6
In this case, specialized knowledge of processes, and specific knowledge of the effect of certain regulatory actions on parts of the vector Y (i.e. knowledge about T) are possessed by the regulators. No regulator has complete knowledge about T, but taken together, their knowledge about T is nearly exhaustive. Each regulator has detailed knowledge about its "own" part of T, and a relevant portion of Y. However, Y is a vector, and there are mutual constraints among its elements. Thus, decisions which keep R(1)'s visible variables within acceptable limits will drive variables opaque to R(1) out of range. The states of Y and E when they reach R(2), R(3), . . .R(m) may be so badly out of range, or the prior regulatory choices made might so constrain the options of subsequent regulators as to render the variety of the subsequent regulators inadequate to the task of bringing the variables back within limits. It may be that those regulatory actions which R(m) could use to bring its variables back into range would send other variables out of range. Iteration back through one or more regulators might or might not rectify the system in any finite period of time.
Complicating matters, some variables (elements of Y) might be partially or wholly functions of the time (or number of iterations) required to produce a result within the specified limits of E. Remembering that, taken together, the total knowledge of the regulators is sufficient for success, there may be an alternative way of configuring the regulation to make it more efficient.
Consider the case where the regulators are taken out of series and configured in a fully connected heterarchy, using the principles of the homeostat (veto power), and principles of the non-error controlled regulator (in effect modeling the system), vastly improved performance will result.
The following might represent the dynamics of such a system:
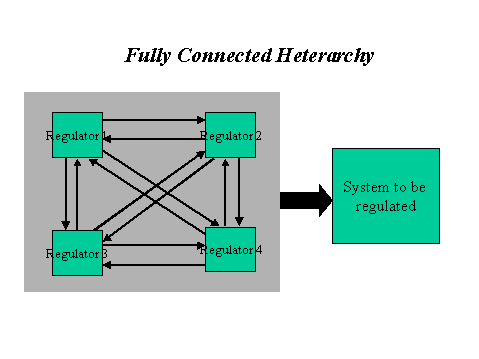
Figure 7
The significance of this conclusion is that the configuration of the regulators alone improves the effectiveness of regulation. If together they have requisite variety then improvement will come from their dynamic configuration alone. The requirements and problem characteristics have to do with distribution of knowledge. In this case, not only is Aulin's solution of a governing hierarchy unjustified17, but given that the sum of HD(Rm)=0, the heterarchical configuration is the only efficient solution, considerably more efficient than any sequential configuration.
Sequential processing, even when governed, is far less efficient than heterarchy with simultaneous "cause controlled" processing. Sequential processing is in effect error controlled regulation. Ashby has shown that error controlled regulation must contain some error, i.e. the regulation cannot even in theory be perfect.
There is further evidence that this solution is the preferred one from the perspective of optimality, and this evidence gives us further specification regarding the dynamic configuration of such a regulatory scheme. Conant and Ashby have proven that "Every good regulator of a system must be a model of that system."18 Considering the situation "in which the set of regulatory events R and the set of events S in the rest of the system jointly determine . . . the outcome Z. By an optimal regulator we will mean a regulator which produces regulatory events in such a way that H(Z) is minimal . . . ."19 Their account is as follows:
"The simplest optimal regulator R of a reguland S produces events R which are related to the events S by a mapping h: S-->R.
"Restated somewhat less rigorously, the theorem says that the best regulator of a system is one which is a model of that system in the sense that the regulator's actions are merely the system's actions as seen through a mapping h. . . .
"The theorem calls for several comments. First it leaves open the possibility that there are regulators which are just as successful (just as optimal) as the simplest optimal regulator(s) but which are unnecessarily complex. In this regard, the theorem can be interpreted as saying that although not all optimal regulators are models of their regulands, the ones which are not are all unnecessarily complex.
"Second, it shows clearly that the search for the best regulator is essentially a search among the mappings from S into R; only regulators for which there is such a mapping need be considered. . . .
"Last . . . if the statistics of p(S) changes, the mapping h will change appropriately, so that the best regulator in such a situation will still be a model of the reguland, but a time-varying model will be needed to regulate the time-varying reguland."20
To model a process, a representative of every constraint on that process must be represented. When constraints are multiple, depending on values of a variety of variables, then regulators who possess the variety of knowledge must be included on the team to enable the accurate modeling of the process to be designed. Aspects of this process resemble conditions in the homeostat. If governors on the homeostat were to set parameter values inflexibly, without having perfect knowledge of the solution, the system might well be forced into an unstable condition.21 With an enormous number of conditional constraints among variables in the Y-vector, the knowledge required to make effective decisions a priori becomes astronomical. An inappropriate early choice, sequentially, might drive the system to instability. It will also limit the variety of acceptable configurations and therefore the chances of success (stability). Pragmatically, if carrying out a planning process, there is always the option, and the associated costs, of restarting from new initial conditions.
The principles of improvement of regulatory processes have been presented. It will be useful now to look at the theory of amplification of regulation. The limits of regulation have inherently to do with the limited capacity of a single regulatory entity for variety. Aulin has suggested that a series of governors imposed on top of the first line regulators is necessary to improve regulation performance, if it can be improved upon at all. (until first line regulators can become "self regulating".) Yet, imposing governors (and sometimes governors on top of governors) on top of first line regulators to modify the latter's performance is an activity having diminishing returns. How quickly the returns diminish depends in part on the distribution of the necessary knowledge of T over the regulators and governors.
Ashby has in mind something considerably more powerful than the linear improvement of a system's regulatory performance when he discusses the amplification of regulation: he is interested in orders of magnitude of improvement, and how it might be obtained from regulators who are themselves so limited. The secret of this improvement in regulatory capacity is the ability of a regulator "A" to design a much more potent regulator "B", which may transcend the limitations of "A", so long as a sufficient amount of additional power or energy is supplied to "B". He cites examples such as the design of power tools, automatic mechanisms such as an air conditioner or temperature controlled water baths. Each of these regulate more--more often, in more detail, more effectively, or more efficiently--than the original regulator, the designer.22
A yet more powerful example can be found in living organisms.
The gene pattern, as a store or channel for variety, has limited capacity. Survival goes especially to those species that use the capacity efficiently. It can be used directly or indirectly.
The direct use occurs when the gene pattern is used to specify the regulator . . . (in the embryo) and the organism passes its life responding to each disturbance as the gene pattern has determined. Amplification does not occur (from our present point of view, though some advantage is gained. . . .)
The indirect use occurs when the gene pattern builds a regulator (R1) whose action is to build the main regulator (R2) [the cerebral cortex, itself an adaptive mechanism]. . . .
. . . The amplification of regulation is thus no new thing, for the higher animals, those that adapt by learning, discovered (sic) the method long ago. 23
One configuration of this mechanism is certainly hierarchy of the nature of the master-slave relationship, the social hierarchy proposed by Aulin, or the hierarchy in the relationship of a human to his/her power tools. However, Ashby points out that the homeostat could be looked at as just this kind of mechanism. "Part B of the homeostat was built, and thus became the primary regulator R1. Coupled to Part A, it acts so as to cause A to become stable with its needle in the centre. When this is achieved, A acts as a regulator (R2) toward the disturbances coming into it that would make the needles diverge. Though R2 of this particular example is extremely simple, nothing in principle separates this case from those in which the regulator R2 is of any degree of complexity."24 Thus heterarchy, in the form of mutual dynamic constraints, is a perfectly acceptable form of amplification of regulation.
Thus, dividing a regulation into two or more stages enables the expansion of regulatory capabilities. Making the second or subsequent stages adaptive mechanisms, rather than just error-control mechanisms, opens the possibility of orders of magnitude more control. However, we should not get carried away with the potential of the adaptive mechanisms without also noting the nature of adaptation. There is a serious drawback to simply designing an adaptive mechanism and allowing it to run, if our aim is control toward a particular end or direction which we wish to specify, as distinguished from the organism's internally perceived "needs". This might be referred to as the Frankenstein effect. How, then, can these powerful adaptive mechanisms be controlled?
It will now be necessary to examine the mechanism of adaptation. First, Ashby notes that almost every "machine" (info-tight dynamic system) will be self organizing in that it will run until it gets to an equilibrial state (or set of equilibrial states) including limit cycles etc. However that state is not necessarily the one which may, from a particular point of view, be desirable. He says: "We must accept that: (1) most organizations are bad ones; (2) the good ones must be sought for: and (3) what is meant by "good" must be clearly defined, explicitly if necessary, in every case."25
A good organization in biology means the achievement of some "focal condition" involving the survival of the organism, and (over the longer perspective), the survival of the species. In engineering, it means the performance of, say, an antenna which transmits and receives over not just some frequency, but the particular frequencies for which it will be used. In a manufacturing organization, a "good" organization will be one which permits the firm to obtain and maintain market share, and turns at least sufficient profits to continue to operate.
However, a "good" organization of anything may become a "bad" organization without changing its internal structure. All that needs to change is the environment. For instance, field mice have evolved an instinctive behavior which causes them to freeze in position at the first sign of danger. This was a "good" response when they were attempting to avoid predators such as owls, which relied largely on the perception of movement to identify and locate their prey. When they were used as laboratory animals, however, this became a "bad" organizational feature. Physiological psychologists placed them on grids and delivered electric shocks to them to train them in certain kinds of behavior patterns. Their instinctive reaction -- to freeze rather than flee to avoid the unpleasant stimulus -- caused their deaths. (On the other hand, it also caused enormous frustration for the laboratory scientists who eventually stopped using the species for experimentation. In that sense, perhaps it was a "good" response for the species, though not for the individual experimental mouse.)
Now let us turn explicitly to the adaptive mechanism in organisms.
"The organism which can adapt thus has a motor output to the environment and two feedback loops. The first loop consists of the ordinary sensory input from eye, ear, joints, etc., giving the organism non-affective information about the world around it. The second feedback loop goes through the essential variables. . . ; it carries information about whether the essential variables are or are not driven outside the normal limits."26
"The basic rule for adaptation by trial and error is: If the trial is unsuccessful [i.e. fails to bring the essential variable back into range], change the way of behaving; When, and only when, it is successful, retain the way of behaving."27
Consider Ashby's example of a kitten approaching a fire for the first time. It is aware of the flame, the warmth, the fireplace through its normal sensory inputs. This is loop 1. It approaches the fire and bats at the flame or the embers, burning its paw, and thus driving its "essential variable" skin temperature outside its normal limits (loop 2). It jumps back or sideways, away from the source of pain. Subsequently, it avoids the non-affective configuration of perceptions it has associated with being burned, i.e. the heat near the fire, or the fireplace itself.
This configuration develops behaviors which, after adaptation, eliminate the need for error controlled regulation in favor of "cause-controlled" regulation. This is because they behave in response to the proximal non-affective information about the environment (e.g. the presence of fire) rather than in response to the error (e.g. venturing into the fire and being burned).
In "higher" behavior, the realm of human social and interpersonal motivation, we no longer deal with physiological "essential variables" but expectations, desires and the like. William Powers28 has stated and provided extensive evidence for his thesis that, in psychological terms, "behavior is the control of perception." This means that an organism will act and react to changes in its environment or experience until its perceptions are consonant with its "reference signal", that which it expects or desires. It should be noted that though this is a description of an error controlled system, it can be made almost isomorphic to Ashby's adaptive system (minus step-mechanism requirement) if it is assumed that it can associate relevant non-affective information from its environment with its perceptions relative to reference signals.
Using Adaptive Systems as Regulators
However, the purpose of considering how adaptive mechanisms adapt to achieve the goal state of their own survival, and to the satisfactions of their own reference signals is not of primary importance to this argument. What is critical to the present study is how the adaptive mechanisms behave in support of goals of a larger system in which they participate. The essential variables or reference signal of a particular adaptive system may or may not be congruent with nor fully supportive of the overall system goal, or of the goals of the "designer". Thus, it is time to address how such complex mechanisms must be co-ordinated to achieve a desired goal of the larger enterprise.
This situation might be diagrammed as follows:
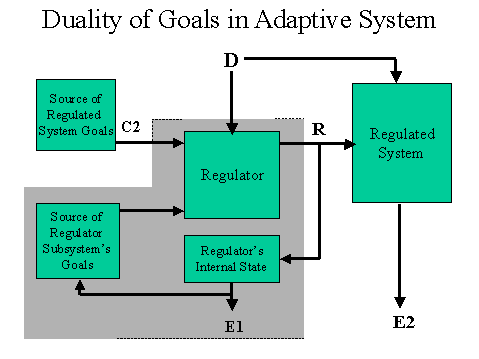
Figure 8
In this case, the action R of the regulator has two consequences: One to the regulated system, resulting in output E2; and one to the regulator unit or organism itself, output E1, which is associated with its essential variables or reference signal. We may suppose that the regulator generates the choice of R based on some arbitrary rule; however, it might be argued that the following two rules will come close to an actual rational strategy.
If there is a conflict between achieving the goals given by C1 and C2, the regulator will choose R based on C1, its internal goals or reference signal. If there is no conflict between achieving the goals given by C1 and C2, it will choose based on C2.
The combination of D and R not only affect E2, the system variables, but also may have an impact on E1 the person or psychology of the individual carrying out the role of the regulator R. There is no formal reason for E1 to have a relationship with E2. Unless they are related in some systematic way, however, the regulator's acts will have an arbitrary effect on the regulated system.
If there are no immediate effects on the regulator as a consequence of the regulator's choice of a less than best effect on the system, the regulator still may get feedback from the "Source of Regulated System Goals." This feedback may come in terms of information (C2), or in terms of physical and emotional consequences, impact on the regulator's desired state (probably through D). Feedback through C2 will not alone change the regulator's behavior, since it has not impacted the rules by which the regulator operates. Indeed, if the regulator were to operate against its own best interests, it would cease to be a viable adaptive system itself. It will be effective only if the choice was due to ignorance on the part of the regulator. If the feedback through D is not forthcoming, is inappropriate, or is separated too long in time from the regulatory choice, appropriate adaptation of R in terms of the goals of the system (E2) will not be possible.
Moreover, looked at from the point of view of the system, the system is behaving as an error-control mechanism with respect to controlling the output of the regulator. As we have seen, the regulatory mechanism is error controlled, and so can never be perfect. It also requires (and must continually monitor) constant, short-loop feedback to detect "errors" in the regulator's behavior. Since each regulatory (or governing) element of the system, including those monitoring the regulator's behavior, are limited in variety (capacity to process information), more of the system's resources must be allocated to the governing function, instead of to productive system functions. The alternative is to set up governors to restrict the regulator's variety. It has been demonstrated earlier how these "solutions" lead to less efficient regulation.
It might be possible, however, to do something more directly: If it were possible to specify or co-ordinate the relationship between E1 and E2, then the regulator's natural adaptive and adapted response could be utilized to make appropriate choices with respect to system goals without changing R's rules, or diminishing the potential regulatory efficiency in the system. At first, this may seem a daunting task. It appears that the inner workings and psychology of every organism which functions as a regulator in the system must be understood, and a different scheme tailored to each. However, it should be noted first that most of these organisms are remarkably similar in construction and needs. If some general similarities in their requirements are known, much of the detailed knowledge may be unnecessary.
For those outliers and exceptions, one of two things may be done. If the specific organism in question is vital to the organization, a tailor-made scheme might be developed as needed. But it will in general need to be developed only once. Those others who have requirements which cannot easily be met will meet the same consequences as species variants in natural settings: migrate or perish. (Since most of the requirements of R-organisms in the current discussion are psychological rather than physiological, migration to a different environment seems the most likely course.)
Suppose a general policy rule were to be put into effect, such that "If a particular regulatory choice is good for the regulated system, given the regulator's knowledge of the consequences of that choice, then such a choice shall be either made good for the regulator or, minimally, it will have no negative effect." Then, after a short time, regulators R would not need to look to the rules to make a regulatory decision at all. The regulator could simply choose based on C2, controlling for acceptable values of E2. At this point, improvement of regulatory choices would be maximized by ensuring that the regulator had sufficient knowledge of the system's requirements (C2), knowledge of the effects regulatory choices on the system (E2), and the authority to carry out the associated regulatory acts.
Since circumstances do change and evolve, there is a need for continued communication throughout the system, to ensure that the knowledge of all regulators matches current environmental requirements. In order to be maximally effective, communication must take place within a shared vocabulary or technical language. Efficiency is increased in the same way that using a higher level language, such as Pascal or APL, is enormously more efficient than programming in assembler or machine language.
A Note on Hierarchy and Control
As previously discussed, control is distinct from regulation. Control effectiveness lies in the business of setting and communicating parameters for results, and co-ordinating the environment so that the regulators will automatically behave in ways which achieves the system's overall goals. Thus, hierarchy which limits variety in the regulator is misplaced. Hierarchy which looks at a higher level of concern--longer timeframes, strategic evolution, and the like--needs to be in the business of control, but not in the business of regulation.
Summary: Principles of Complex Systems Control
What has emerged from the foregoing theoretical discussion?
1) Error controlled regulation requires a closed feedback loop. In general, the shorter the loop, the more effective the regulation. It should be noted that even regulation designed to be cause-controlled requires a closed feedback loop when disturbances and their relationship to regulatory actions are incompletely known.
2) Regulation can be improved by improving the regulatory capacity of first-line regulators. This improvement includes increasing the relevant variety of regulatory actions on the part of the first-line regulator; granting the authority to act based on the adequacy of the regulator's variety; and removing the regulator's ignorance of the relationship of regulatory actions on outcome. (One prominent method for accomplishing the latter is via closed and short feedback loops.)
3) The most efficient regulation is cause-controlled regulation by a simultaneous regulatory mechanism which can be effectively configured isomorphically to its reguland. In this case, the sub-regulators represent as closely as possible the potential constraints exerted by every part of the system on every other part of the system (or process).
4) To obtain different output from a complex system, the internal structure or process must be adjusted or reconfigured.
5) There is no intrinsic requirement for an "is boss of" hierarchy of regulation in order to increase or amplify regulatory capability. A separate argument must be made for this type of hierarchy requirement. The proper role of hierarchy is in control functions: setting goals and ensuring intrinsic co-ordination. Fewer levels of hierarchy will be required for this function than for a regulatory hierarchy.
6) Regulation can be amplified by the design of a 2 or more stage regulatory mechanism, and further enhanced by making later stages adaptive mechanisms. Additional co-ordination of these adaptive mechanisms is required to prevent the "Frankenstein effect". The co-ordination need not be explicitly governed. To successfully co-ordinate the behavior of a set of adaptive mechanisms, one must have primarily intrinsic control of the "environment." This is the legitimate function of hierarchy. This includes ensuring:
a) a direct and congruent relationship between consequences of regulatory actions on the system and on the consequences to the R-organism;
b) the existence of short feedback loops for both adaptive systems and error controlled regulation processes, containing appropriate measurement information.
c) alignment of the "control" mechanism which gives parameters to Rs, so that the desired regulated outcome are congruent with the requirements for the system output;
d) establishment of a common language to reduce the information transmission requirements of the system.
Back to Table of Contents On to next chapter Back to Home Page