=======================================================================
Cybernetics in the 3rd Millennium (C3M) Volume 17 Number 1, Mar. 2023
Alan B. Scrivener — www.well.com/user/abs — mailto:abs@well.com
========================================================================
 Glass Bead Game worksheet (programmed by author)
In this issue:
Glass Bead Game worksheet (programmed by author)
In this issue:
Short Subjects
 "Fractured Flickers" letterhead with Theda Bara
(artofjayward.blogspot.com/2015/06/fractured-flickers.html)
"Fractured Flickers" letterhead with Theda Bara
(artofjayward.blogspot.com/2015/06/fractured-flickers.html)
- ChatGPT failed my Turing test
There's been a lot of buzz lately about chatbots with "Artificial Intelligence"
that may make mediocre people obsolete. The first to grab headlines was ChatGPT.
( openai.com/blog/chatgpt )
I recalled that Douglas Hofstadter came up with a challenge to test the
intelligence of a chatbot (what we call a Turing Test), to make sense of
these words:
I think it was in Fluid Concepts and Creative Analogies: Computer Models Of
the Fundamental Mechanisms of Thought (1996).
( www.amazon.com/exec/obidos/ASIN/9780465024759/hip0bd )
My interpretation is that these words form a sentence fragment which is both a
joke and a paradox. If you supply the missing verb, "has" or "contained," then
the new sentence is false. But the original partial sentence, if you infer its
meaning, is true. Well, I laughed anyway.
On 14 December 2022 I tried out CHatGPT, and one thing I did was ask it to
diagram the sentence fragment. It said it couldn't draw diagrams.
So I tried again.
Me: Analyze this sentence: "This sentence no verb."
ChatGPT: The sentence you provided is grammatically incorrect
because it does not contain a verb. In order for a
sentence to be grammatically correct, it must have at
least one verb. Verbs are words that describe an
action, state, or occurence, and are often used to
indicate the main activity or event in a sentence.
Without a verb, a sentence is incomplete and can't
convey a complete thought.
So I'd say it flunked, getting neither the joke nor the paradox.
This bot reminds me of a comedy character named Perini Scleroso played by
Andrea Martin on the TV show Second City Television (SCTV).
I was originally going to link to "SCTV PSA - The Illegal Immigrant Problem"
sketch but I thought it hadn't aged well. I needed a warning message
like this one Disney+ has been using:
This programme includes negative depictions and/or mistreatment of people or
cultures. These stereotypes were then and are wrong now. Rather than remove
this content, we want to acknowledge its harmful impact, learn from it and
spark conversation to create a more inclusive future together.
So instead, I found the somewhat less cringeworthy but actually more relevant sketch .
ChatGPT has been compared to a parrot with a very good memory that has listened
to a million years of radio. I see it more resembling Perini.
And speaking of warning labels, these chatbots have a prrennial problem of being
"inappropriate," because they've sucked up the internet, toxicity and all. If
I were a Nazi, or a frat boy prankster, or an agent of some foreign or
corporate power with an agenda for sabotage, I'd flood the internet with
radioactive content to corrupt the bots. I mean terabytes. Of course I
wouldn't be able to write it all, so I'd have bots dot it.
- SageMath software
I've been reading the excellent systems theory textbook Modeling Life:
The Mathematics of Biological Systems (2017) by Alan Garfinkel, Jane
Shevtsov and Yina Guo.
( www.amazon.com/exec/obidos/ASIN/3319597302/hip0bd )
It used the SageMath software in the creation of the text, and also has
students use it. I downloaded it and made my first plot, with the command:
show(plot(sin(x) + sin(1.6*x), 0, 40)).
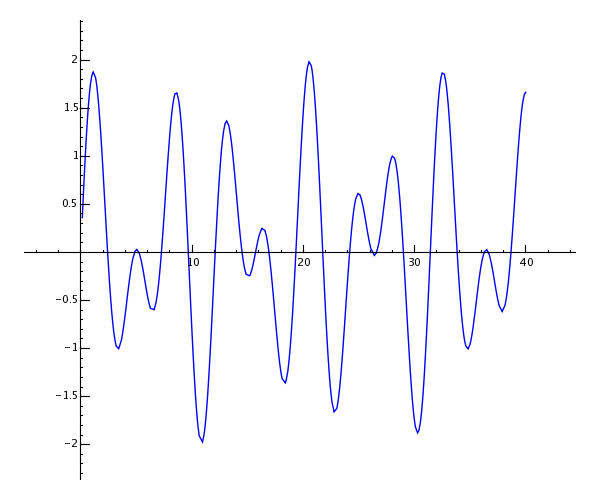 Free from sagemath.org.
Plot command taken from "A Tour of Sage."
Free from sagemath.org.
Plot command taken from "A Tour of Sage."
- Summer of Math Exposition (SoME) 2022
Brad Sanderson of 3blue1brown and others did a second contest last summer for
math explainer videos.
( www.youtube.com/watch?v=cDofhN-RJqg )
A Glass Bead Game
 glass beads from Beads Factory
( beadsfactory.com )
glass beads from Beads Factory
( beadsfactory.com )
I've invented a game and you're invited to play. It's like a competitive
puzzle, involving multicolored glass beads strung on a series of cords.
THE INSPIRATION FOR THE GAME
In a previous eZine, "Cybernetics in the 3rd Millennium volume 2 number 1" (Jan. 2003)
(
people.well.com/user/abs/Cyb/archive/c3m_0201.html )
I wrote:
Psychedelic guru Timothy Leary's last book, "Chaos & Cyber Culture"
(1994), was a collection of his recent short writings.
( www.amazon.com/exec/obidos/ASIN/0914171771/hip0bd )
In one essay he talked about Hermann Hesse, whose "Siddhartha" (1922),
and "Steppenwolf" (1927) were counter-culture favorites in the 1960s:
Poor Hesse, he seems out of place up here in the high-tech,
cybercool, Sharp catalog, M.B.A., upwardly mobile 1990s.
But our patronizing pity for the washed-up Swiss sage may be
premature. In the avant-garde frontiers of the computer culture,
around Massachusetts Avenue in Cambridge, around Palo Alto, in
the Carnegie-Mellon A.I. labs, in the back rooms of the
computer-graphics labs in Southern California, a Hesse comeback
seems to be happening. This revival, however, is not connected
with Hermann's mystical, eastern writings. It's based on his
last, and least-understood work, "Magister Ludi, or The Glass
Bead Game."
( www.amazon.com/exec/obidos/ASIN/022461844X/hip0bd )
This book... is positioned a few centuries in the future, when
human intelligence is enhanced and human culture elevated by
a device for thought-processing called the glass bead game.
Up here in the Electronic Nineties we can appreciate what Hesse
did at the very pinnacle (1931-42) of the smoke-stack mechanical
age. He forecast with astonishing accuracy a certain
postindustrial device for converting thoughts to digital
elements and processing them. No doubt about it, the sage of
the hippies was anticipating an electronic mind-appliance that
would not appear on the consumer market until 1976.
I refer, of course, to that Fruit from the Tree of Knowledge
called the Apple Computer.
Hesse described the glass bead game as "a serial arrangement, an
ordering, grouping, and interfacing of concentrated concepts of
many fields of thought and aesthetics. ...the Game of games had
developed into a kind of universal language through which the
players could express values and set these in relation to one
another."
This sounds to me remarkably like Wolfram's vision of the
significance of Cellular Automata.
I'm not sure I'd go so far as to say Hesse predicted the digital computer,
let alone the home or personal computer, not to mention the particular brand
of Apple computers. But I think it's fair to say he predicted digital encoding.
 Jacquard Loom card maker from Manchester Science and Industry Museum
( https://www.scienceandindustrymuseum.org.uk/objects-and-stories/jacquard-loom )
Jacquard Loom card maker from Manchester Science and Industry Museum
( https://www.scienceandindustrymuseum.org.uk/objects-and-stories/jacquard-loom )
The world at the time of his writing (1943) already had the Jacquard Loom (1804),
which encoded thread colors on punch cards in weaving,
the designs of gear-based digital computation of Charles Babbage (1822),
the tabulating machines of Herman Hollerith which were used in the 1890 census,
 Harvard Mark I from Wikimedia Commons
Harvard Mark I from Wikimedia Commons
and early experimental electromechanical relay and vacuum tube digital computers,
as well as a number of then-classified digital machines of various types for
wartime codebreaking, but Hesse probably would have been unaware of them.
But he did envision an ability to use finite beads to express concepts and
patterns in the sciences in the arts. The idea of all forms of data being
stored in interactive computers was familiar to every Star Trek fan in 1966,
but many futurists and business planners didn't believe until the late 1980s
that it was going to actually happen.
Hesse didn't describe the Glass Bead Game in detail, using the concept as a
plot device and a metaphor, to make points about social and political issues,
especially his disdain for hyper-academic pursuits and fascism. At the end of
novel he even delved into alternate universes.
An on-line plot summary
gives some features of the game that we do learn from the book:
- it is suggested that the rules are too complex for a lay audience to understand
- to play the game at all requires years of study in mathematics, music, and history
- play proceeds when players make conceptual connections between topics that
seem unrelated on the surface
WIkipedia elaborates:
"The Glass Bead Game is 'a kind of synthesis of human learning' in which themes,
such as a musical phrase or a philosophical thought, are stated. As the Game
progresses, associations between the themes become deeper and more varied.
Although the Glass Bead Game is described lucidly, the rules and mechanics are
not explained in detail."
I figured that this vagueness gave me enough leeway to invent something.
THE MECHANICS OF THE GAME
 weaving pattern from weave-away.blogspot.com
weaving pattern from weave-away.blogspot.com
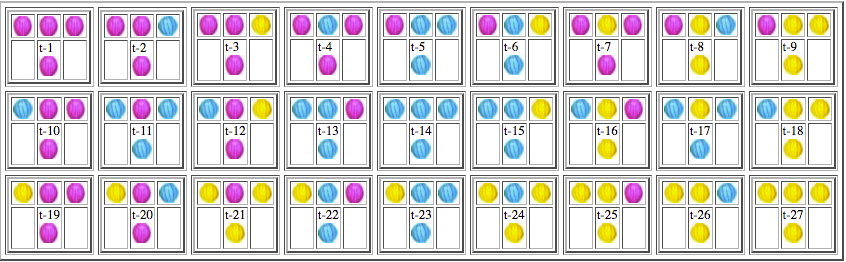
What I've come up with is this: the Game Master gives the players a challenge.
They are presented with two strings of colored beads of the same length
which have different patters of colors. One is called the beginning pattern
and the other is the target pattern.
| beginning pattern: |
 |
 |
 |
 |
 |
 |
 |
|
| target pattern: |
 |
 |
 |
 |
 |
 |
 |
|
example beginning and target patterns in a three-color game
Each player can do three types of things to transform one into the other.
In order of least to most "costly" in the scoring, they can
(1) apply a rule,
(2) change the rule they are using, or
(3) change a single bead color.
The rules available are taken from the mathematical concept of a cellular automaton.
Webster defines the word as a mechanical device, but to mathematicians it can
refer to a type of finite state machine.
I described the basic form of a simple cellular automaton in "What Hath Wolfram
Wrought?" C3M volume 1 number 2, October 2002.
(
people.well.com/user/abs/Cyb/archive/c3m_0102.html )
The particular cellular automaton that the most number of people are familiar
with is "Conway's Life," also called the Game of Life.
 sample snapshot from Conway's Life
sample snapshot from Conway's Life
This is a two-state, two-dimensional system in which each cell changes based
on its previous value and those of its neighbors. A multitude of web versions
exist of you want to play with it.
(
playgameoflife.com )
But Wolfram focused on the simplest non-trivial cellular automaton, a
two-state one-dimensional system that looks at the current state and the
two nearest neighbors in computing each following step. This is the model
I am using initially for this Glass Bead Game.
The following page from Wolfram's "A New Kind of Science" shows a time history
of one of these machines, where each row is a single step and time moves downward.
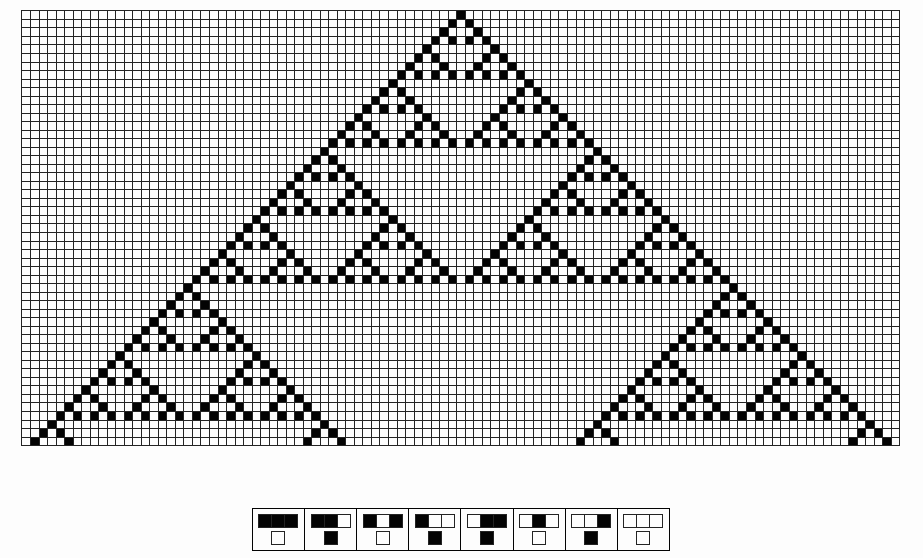 cellular automaton from "Introduction to A New Kind of Science"
( www.stephenwolfram.com/publications/introduction-to-a-new-kind-of-science )
cellular automaton from "Introduction to A New Kind of Science"
( www.stephenwolfram.com/publications/introduction-to-a-new-kind-of-science )
At the bottom is a key to the rule used. (I will be representing a white cell
as 0 and a black cell as 1, per Wolfram.) You read the key from left to right
as saying:
- if the left neighbor is 1, the current cell is 1, and the right neighbor
is 1, make the new cell 0
- if the left neighbor is 1, the current cell is 1, and the right neighbor
is 0, make the new cell 1
...and so on. Wolfram also suggests taking the bottom row of this key and
encoding the rule number in binary. In the case it would be 01011010, or
90 in base ten.
I've created a worksheet you can use for encoding and decoding rules:
(
people.well.com/user/abs/Cyb/archive/GBG_RULE_WORKSHEET_2.html )
A player makes a move by informing the Magister Ludi that they are either taking
one time step, changing to a new rule number, or modifying a certain bead color.
My current approach to scoring is this: given S is the size of the bead strand,
a step is 1 point, a rule change is S squared points, and a bead change is S
cubed points. Low score wins.
I am willing to take suggestions on this, based on analysis and game play.
One final detail of the rules is what to do at the left and right edges.
The mathematical abstraction of this family of cellular automata sometimes
allows the width of each row to be infinite, but for the game I've designed
there will always be a finite bead strand length, so there will always be two
ends, which must be handled specially. There are two I allow: first, called
"wrap," where the strand wraps around into a necklace of sorts, and so the bead
to left of the leftmost one displayed is assumed to be the same as the rightmost
displayed bead, and vice versa. Another way of thinking about this is that the
strand is infinite but always repeats exactly the finite pattern.
The second is "no wrap," in which the leftmost bead is assumed to have an unseen
left neighbor which is a "dead" bead (always 0, or white) and the rightmost bead
is also assumed to have an unseen right neighbor which is also a "dead" bead.
So at the beginning of a game, the player specifies wrap or no wrap. They
are allowed to change this during play at the same score cost as a rule change.
After so much abstraction perhaps an example will help. Here is a challenge
in which the Magister Ludi provides a seven bead game, to change 1000101 binary
(69 decimal) into 0111110 binary (126 decimal).
example Glass Bead Game
key: | bead | digit |
|---|
 | 0 |
 | 1 |
| | | color | meaning |
|---|
| light green | start beads |
| pink | target beads |
|
wrap ; starting beads = 1000101 ; target beads = 0111110
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
step or
action |
rule/bit
number |
binary
beads |
 |
 |
 |
 |
 |
 |
 |
input |
- |
1000101 |
 |
 |
 |
 |
 |
 |
 |
1 |
90 |
1101001 |
 |
 |
 |
 |
 |
 |
 |
2 |
90 |
0100111 |
 |
 |
 |
 |
 |
 |
 |
3 |
90 |
0011101 |
 |
 |
 |
 |
 |
 |
 |
4 |
90 |
1110100 |
 |
 |
 |
 |
 |
 |
 |
5 |
90 |
1010011 |
 |
 |
 |
 |
 |
 |
 |
6 |
110 |
1111100 |
 |
 |
 |
 |
 |
 |
 |
7 |
110 |
0000111 |
 |
 |
 |
 |
 |
 |
 |
8 |
110 |
1001001 |
 |
 |
 |
 |
 |
 |
 |
9 |
110 |
1111110 |
 |
 |
 |
 |
 |
 |
 |
flip |
1 |
0111110 |
target found; steps (1 point): 9; rule/wrap
changes (49 points): 1; bit flips (343 points): 1
score = 401
|
In this game the player uses wrap, and starts with rule 90 applied 5
times, resulting in 1010011 (83). They then apply rule 110 four times
to get 1111110 (126). Lastly they flip bit 1 to get 0111110 (62), the target.
As shown the score is 401. I don't know if this is a well-played game or not,
so I offer:
Challenge Number One: What is a better scoring
game using these beginning and target bead patterns?
In the future I would like to expand to more than two bead colors.
I have created a worksheet for a three-color (trinary) Glass Bead Game.
(
people.well.com/user/abs/Cyb/archive/GBG_RULE_WORKSHEET_3.html )
While this will produce a more colorful and complex game, it will vastly
increase the computing requirements and possibly expand it beyond human
comprehension. For the binary (two state) game has only
256 rules, given by:
The number of trinary (three state) rules: is
7,625,597,484,987
(that's trillion with a t), given by:
Wolfram has said that he has a filing cabinet with 256 folders for the 256 rules
of the 2D 2-state cellular automaton, and in each are scientific papers about
that rule. He claims they all have been studied and have uses in mathematics
and related applied mathematical fields. We can be confident he doesn't
have 7+ trillion folders for the 3-sate rules.
THE CHALLENGE OF THE GAME

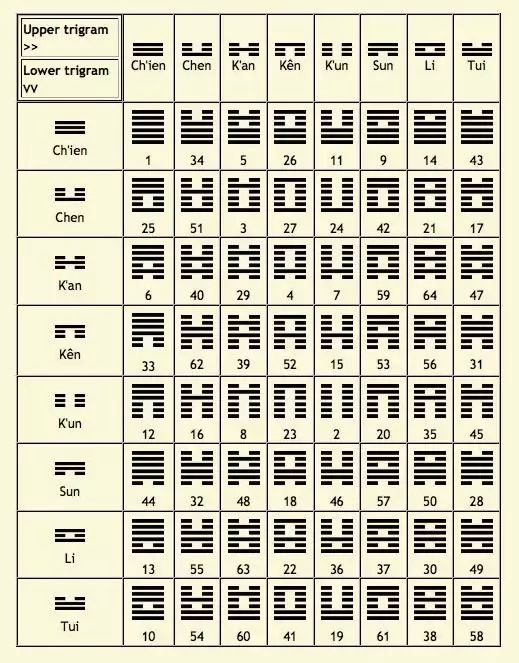 the beginning of Beethoven's Fifth I Ching hexagrams
the beginning of Beethoven's Fifth I Ching hexagrams
Since Hesse's Glass Bead Game is supposed to relate patterns in the arts and
sciences, in fact all of human culture and the natural world, I thought I would
issue a nontrivial challenge involving taking a pattern from Beethoven's music
and transforming it into a pattern from a book of Chinese philosophy.
For the Beethoven I chose the beginning of his 5th Symphony, just the melody
(which I selected subjectively). I use the first 7 measures or so. I transcribed
it from 2/4 time thusly (lines are measure marks):
eighth note rest
eighth note G
eighth note G
eighth note G
----
half note E
----
eighth note rest
eighth note F
eighth note F
eighth note F
----
whole note D (two measures)
----
----
eighth note rest
eighth note G
eighth note G
eighth note G
----
half note C
I created a nine-bit code for each note or rest:
+-+-+-+-+-+-+-+-+-+
|dura |fsr| note |
+-+-+-+-+-+-+-+-+-+
Three bits for duration, two bits for flat/sharp or rest, and four bits for pitch.
| duration
000 = S = sixteenth note
001 = E = eighth note
010 = Q = quarter note
011 = H = half note
100 = W = whole note
flat/sharp or rest
00 = Z = rest
01 = b = flat
10 = # = sharp
11 = = none of the above
pitch
000 = Z = rest
0001-0111 = A-G = Treble notes
1001-1111 = a-g = Bass notes
|
This may not be the ideal coding; there are some duplicate ways to specify
some notes, such as middle C, and some patterns are impossible, such as
certain flats and sharps, and it only has a two octave range, but it will
suffice. (Note that all nine zeroes is a sixteenth note rest, and any number
ending seven zeroes is some duration of rest. This is wasteful, but there
is room to improve.)
Converting the above notes to abbreviations, and then to the binary patterns,
separated by colons for clarity, we get:
EZ 001:00:0000
EG 001:11:0111
EG 001:11:0111
EG 001:11:0111
---------------
HE 011:11:0101
---------------
EZ 001:00:0000
EF 001:11:0110
EF 001:11:0110
EF 001:11:0110
---------------
WD 100:11:0100
---------------
---------------
EZ 001:00:0000
EG 001:11:0111
EG 001:11:0111
EG 001:11:0111
---------------
HC 011:11:0011
Concatenating the binary patterns separated by hyphens we get:
001:00:0000-001:11:0111-001:11:0111-001:11:0111-
011:11:0101-001:00:0000-001:11:0110-001:11:0110-
001:11:0110-100:11:0100-001:00:0000-001:11:0111-
001:11:0111-001:11:0111-011:11:0011
and lastly removing the colons and hyphens we get the binary number:
001000000001110111001110111001110111011110101001000000001110110001110110001110110100110100001000000001110111001110111001110111011110011
In decimal (base ten):
5464328830608862715843142692626669301491
So that is our beginning bead pattern.
For the target bead pattern I take the order of bits given by the patterns
in the I Ching, a book of Chinese philosophy and fortune telling. It dates back
three thousand years, and according to a story Leibniz studied it and then
invented binary numbers.
In the image above the basic three-bit units called tri-grams are shown, where
a broken line is a 0 and a solid line is a 1. Each pair of trigrams forms a
hexagram, and they are listed in the book in an unusual order; no one knows
exactly why. I used the six bit patterns, concatenated in the order of the hexagrams
shown in the book (Wilhelm translation 1950), to generate the first 135 bits.
For example, hexagram 1 is Ch'ien (Heaven) repeated twice, each shown as three
solid lines or 111. So the first hexagram is 111111, and that's how our target
strand of beads begins. The second hexagram (at position row 5 column 5 in the
diagram) is K'un (Earth), three broken lines or 000, repeated twice, so the
second hexagram is 000000, and that's how our target strand of beads continues.
Strung together, and truncated to 135 beads to match the length of the Beethoven
notes, the entire target value is:
111111000000010001100010010111111010000010010000110111111011000111111000111101101111000100001000011001100110000011110000101001100101100
In decimal (base ten):
42878492080351011745442049171445450822444
Challenge Number Two: What is the best scoring
game using these 135-bit beginning and target bead patterns?
(If you need help converting between bases, like binary and decimal, you can
use the on-line wolframalpha.com and just type, for example, "1000101 binary
to decimal" and it will print 69.)
HOW TO PLAY
If you like you can email me ( abs@well.com ) with your entries. Put "C3M GBG"
in the subject so I'll know.
Include the following info:
- Which challenge are you responding to?
- What is the strand size in beads?
- What are the beginning and target patterns (use any base you like)?:
- What are the initial rule and wrap/no wrap?
- Exactly what actions do you take to reach the target (step, rule or wrap change, bit flip)?
(If you use the program described below, please include the command line and the gbg script file
that you used, explained soon.)
You have enough information above to do it all on paper (hint: print out copies
of the 2-D worksheet and use them). Or, you can use
gbg.py
(for Glass Bead Game), a program I wrote in Python.
I wrote it using Python version 2.7.16, though it should work with other 2.7
versions. The source code and some sample files are located on my web site.
(
people.well.com/user/abs/swdev/Python/gbg )
Follow the link for a directory listing something like this:
Index of /user/abs/swdev/Python/gbg
Name Last modified Size
Run4 26-Mar-2023 23:05 1.7K
RunExample7S 26-Mar-2023 22:59 316
gbg.py.txt 24-Mar-2023 22:29 17K
gbg_ALL.sh.txt 22-Mar-2023 14:40 19K
Apache Server at people.well.com Port 443
There you will find the program, with a
.txt suffix to make it easier
to download, and also some sample shell scripts for running the program and
sample gbg scripts for game play (explained below). Also a single file:
gbg_ALL.sh
which is a self-extracting shell archive of the other files, if you know what
that is. If not, the internet will explain.
That reminds me, to use these tools you will also need a UNIX or Linux shell,
such as
bash (the Bourne again shell) or
csh (the C shell). If you are on a
Mac or UNIX/Linux system, you already have these. If you are on Windows you
can get the GNU foundation tools from Cygwin.
(
www.cygwin.com )
The sample shell scripts are for the C Shell, but can easily be converted to the
Bourne Again SHell.
The resulting HTML file will reference these image files:
 zero.png
zero.png
 one.png
one.png
Right click to download them, or supply your own.
You can run the
gbg program in two modes:
game play (scripted) mode and
exploration
mode. When you run the program and use the
-h "help" flag like so:
You get this help, which unfortunately mixes flags from both modes:
|
usage: gbg.py [-h] [-D] [-A] [-X] [-b BINARY_START] [-f FINAL_BINARY]
[-m MAX_STEPS] [-n NUM_STEPS] [-r RULE] [-s SIZE]
[-t TABLE_FILE] [-L] [-T] [-S] [-W]
explore or play the Glass Bead Game; see:
https://people.well.com/user/abs/Cyb/archive/c3m_1701.html#sec_1
optional arguments:
-h, --help show this help message and exit
-D, --DEBUG debug write
-A, --ABBREV abbreviated output (no beads)
-X, --XOR xor current and target and count bits
-b BINARY_START, --binary_start BINARY_START
starting bead pattern in binary
-f FINAL_BINARY, --final_binary FINAL_BINARY
final bead pattern in binary
-m MAX_STEPS, --max_steps MAX_STEPS
maximum number of steps
-n NUM_STEPS, --num_steps NUM_STEPS
number of steps to print
-r RULE, --rule RULE rule number of 2D binary cellular automaton
-s SIZE, --size SIZE size of string of beads
-t TABLE_FILE, --table_file TABLE_FILE
table file
-L, --Loop stop when loop detected
-T, --Target_stop stop when target reached
-S, --Script take script commands from standard input
-W, --Wrap wrap each line
|
This is useful for jogging your memory, but to explain the program workflow I need to
break it down. In both modes you can use these flags (each flag is shown is short and long
form, such as
-D and
--DEBUG.)
|
-D, --DEBUG debug write
I recommend you don't use this.
-b BINARY_START, --binary_start BINARY_START starting bead pattern in binary
Beginning bead patterns such as 1000101
-f FINAL_BINARY, --final_binary FINAL_BINARY final bead pattern in binary
-s SIZE, --size SIZE size of string of beads
-W, --Wrap wrap each line
Default is no wrap; this flag changes to wrap.
-A, --ABBREV abbreviated output (no beads)
Default is beads displayed as images; this flag suppresses that.
-X, --XOR xor current and target and count bits
This option adds a measure of how "close" the current pattern is to the target,
by counting the number of bits that differ. It uses a bitwise exclusive or
operator, which is like a bit-by-bit "not equals" calculation.
-n NUM_STEPS, --num_steps NUM_STEPS
number of steps to print
When there's a lot of computation you can suppress output beyond a number of steps
|
Exploration mode lets you start with a pattern and evolve it with a single rule, searching
for loops along the way (which mean the pattern will never reach the target).
In this mode you can also use these flags:
|
-m MAX_STEPS, --max_steps MAX_STEPS maximum number of steps
-r RULE, --rule RULE rule number of 2D binary cellular automaton
-t TABLE_FILE, --table_file TABLE_FILE table file
This option allows you to capture beginning bead pattern, final bead pattern, number of
steps and rule number, when the target is reached, as four comma-delimited values in a
designated file. If the target is not found by MAX_STEPS a "U" is placed in the steps field.
-L, --Loop stop when loop detected
Stats are printed out.
-T, --Target_stop stop when target reached
Stats are printed out.
|
In game play (scripted) mode you are trying to win the game and provide a script file
with your commands to do so. You invoke it with the
-S flag:
|
-S, --Script take script commands from standard input
|
Here is the format of the gbg script file
script
command | short for | argument | meaning |
| f | flip | BIT NUMBER | flip a bit (0 becomes 1 or 1 becomes 0) using bit number, counting left to right, one is first |
| r | rule | RULE NUMBER | change the rule number to use going forward |
| s | step | NUMBER OF STEPS | use the current rule to take a number of steps in time |
| w | wrap | 0 (FALSE) OR 1 (TRUE) | wrap/no wrap state |
As an example, this script file was used to produce the example above:
It is run with this command:
|
python gbg.py -D -s 7 -b "1000101" -f "0111110" -S -W > gbg7S.html < script7S.txt
|
STRATEGY
Well, now that I've told you how you
can play the game, perhaps I should give you
some clues as to how you
should play in order to win.
- Fiddling Around
Playing with the rules on paper or with a computer, you quickly find
that rules 0 and 255 annihilate bead patters of any length, turning them
to all zeroes or all ones. There are other rules with simple effects, such
as copying, flipping and shifting bits.
Come to think of it, my first explorations into Conway's Life involved
fiddling around, and I found stable structures (four cells in a square)
+-+-+-+-+
| | | | |
+-+-+-+-+
| |X|X| |
+-+-+-+-+
| |X|X| |
+-+-+-+-+
| | | | |
+-+-+-+-+
2x2 "block" stable structure
and oscillating structures (three cells in a line).
+-+-+-+-+-+ +-+-+-+-+-+
| | | | | | | | | | | |
+-+-+-+-+-+ +-+-+-+-+-+
| | | | | | | | |X| | |
+-+-+-+-+-+ +-+-+-+-+-+
| |X|X|X| | | | |X| | |
+-+-+-+-+-+ +-+-+-+-+-+
| | | | | | | | |X| | |
+-+-+-+-+-+ +-+-+-+-+-+
| | | | | | | | | | | |
+-+-+-+-+-+ +-+-+-+-+-+
3x1 "traffic light" oscillator
- Literature Search
Reading books and later online articles I learned about the complexities of
Conway's Life. I learned about the stable structures called blocks and
boats/beehives, the oscillators called traffic lights or blinkers, the moving
objects called gliders, and the growing patterns called glider guns. I also
learned that a Universal Turing Machine (capable executing all algorithms)
can be built on an infinite Life board.
 A New Kind of Science
The main literature source for 2-D 2-state cellular automata is, of course,
"A New Kind of Science" (2002) by Stephen Wolfram.
( www.amazon.com/exec/obidos/ASIN/1579550258/hip0bd )
Since its publication, though, much has been added to the literature by
enthusiastic researches inspired by the book. In this body of work you will
out about rule 30 being a good random number generator and rule 110 being a
Universal Turing Machine.
Wolfram has also published a follow-on book in 2022, "Twenty Years
of a New Kind of Science," which I am looking forward to reading.
( www.amazon.com/exec/obidos/ASIN/1579550495/hip0bd )
A New Kind of Science
The main literature source for 2-D 2-state cellular automata is, of course,
"A New Kind of Science" (2002) by Stephen Wolfram.
( www.amazon.com/exec/obidos/ASIN/1579550258/hip0bd )
Since its publication, though, much has been added to the literature by
enthusiastic researches inspired by the book. In this body of work you will
out about rule 30 being a good random number generator and rule 110 being a
Universal Turing Machine.
Wolfram has also published a follow-on book in 2022, "Twenty Years
of a New Kind of Science," which I am looking forward to reading.
( www.amazon.com/exec/obidos/ASIN/1579550495/hip0bd )
- Analysis
I analyzed the game starting with its simplest form: a one bead strand.
There are only 2^1 or two possible states, and there are very many ways
to get from one to the other. The weird thing about this category of game
is that most of the cases in the rules are ignored, because in the no-wrap
game the only possible input patterns are 000 and 010 (with the two dead
spots on either end) while in the wrap game the two possible inputs are 000
and 111 (with both ends duplicating the single bead).
I can illustrate this set of games with a directed graph, or digraph (as in
graph theory, also known as network theory). Directed means there are arrows
on the lines. I drew these with the GraphViz program, which is free on the web.
( graphviz.org )
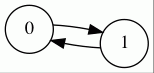 one bead game (both kinds)
This diagram tells us that we can get from any pattern to any other pattern by
applying a single rule for a finite number of steps. In graph theory
nomenclature this graph is known as a complete digraph because every
node has an arrow to every other.
(Note that because there are rules that copy any pattern, every pattern should
have an arrow back to itself. Because this is useless in the game, costing a
point for the step and achieving nothing, I ignore them for the rest of this
article. It makes the diagrams simpler.)
The two bead case gets a little more complicated. There are 2^2 or four
possible patterns. In the no wrap case it is still possible to get from any
pattern to any other with a single rule. Its graph is also a complete graph.
one bead game (both kinds)
This diagram tells us that we can get from any pattern to any other pattern by
applying a single rule for a finite number of steps. In graph theory
nomenclature this graph is known as a complete digraph because every
node has an arrow to every other.
(Note that because there are rules that copy any pattern, every pattern should
have an arrow back to itself. Because this is useless in the game, costing a
point for the step and achieving nothing, I ignore them for the rest of this
article. It makes the diagrams simpler.)
The two bead case gets a little more complicated. There are 2^2 or four
possible patterns. In the no wrap case it is still possible to get from any
pattern to any other with a single rule. Its graph is also a complete graph.
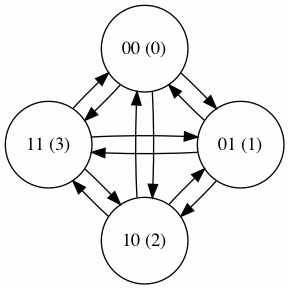 two bead game (no wrap)
But the wrap game with two beads has a problem: if you start with binary 00 or
11 (decimal 0 or 3), whatever you do to create the new bead on the left is also
done to create the new bead on the right. As this diagram shows for starting
pattern 00 binary:
--------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-++-+
|0||0|0||0|
+-++-+-++-+
||a|a||
++-+-++
Whatever the first 'a' ends up being, using the rule for [000] -> [a], the
second 'a' will also end up being. There's no way to break the symmetry and
pick a bead to be different. So the graph looks like this:
two bead game (no wrap)
But the wrap game with two beads has a problem: if you start with binary 00 or
11 (decimal 0 or 3), whatever you do to create the new bead on the left is also
done to create the new bead on the right. As this diagram shows for starting
pattern 00 binary:
--------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-++-+
|0||0|0||0|
+-++-+-++-+
||a|a||
++-+-++
Whatever the first 'a' ends up being, using the rule for [000] -> [a], the
second 'a' will also end up being. There's no way to break the symmetry and
pick a bead to be different. So the graph looks like this:
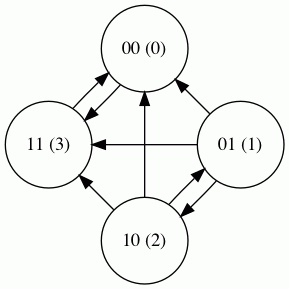 two bead game (wrap)
(A similar argument applies if you begin with 11 binary.)
I'm going to call the states by their decimal numbers from now on for brevity.
If you imagine drawing an oval around 0 and 3, and labeling it A, and then
drawing another oval around 1 and 2, and labeling it B, inside each oval is a
complete digraph. But between the two ovals all of the arrows go from B to A.
Every node in B connects to every node in A, but none of the nodes in A connect
to any nodes in B. In the parlance of systems theory, A is an attractor
of the system.
I did some analysis of the three bead game, but I didn't get entirely correct
answers, as I found when I used Wolfram's Method.
two bead game (wrap)
(A similar argument applies if you begin with 11 binary.)
I'm going to call the states by their decimal numbers from now on for brevity.
If you imagine drawing an oval around 0 and 3, and labeling it A, and then
drawing another oval around 1 and 2, and labeling it B, inside each oval is a
complete digraph. But between the two ovals all of the arrows go from B to A.
Every node in B connects to every node in A, but none of the nodes in A connect
to any nodes in B. In the parlance of systems theory, A is an attractor
of the system.
I did some analysis of the three bead game, but I didn't get entirely correct
answers, as I found when I used Wolfram's Method.
- Wolfram's Method (Exhaustive Search)
By using gbg.py invoked with shell scripts and concatenating
the resulting HTML files I created sets of all possible steps from every pattern
to every other pattern in the 2, 3 and 4 bead cases. I also used the transition
table output, and passed it through another program mapping2matrix.py
(not yet provided; still in work) to get transition matrix for each bead size.
The advantage of this approach is that all secrets are revealed. I fully
mapped all possible games of these bead sizes. The disadvantage is that run
time grow so quickly. The 4 bead case takes about 7 hours. (That's what I
get for using Python, and an old Mac Mini.)
I was able to establish that the 3 bead games, no wrap, also form a connected
digraph.
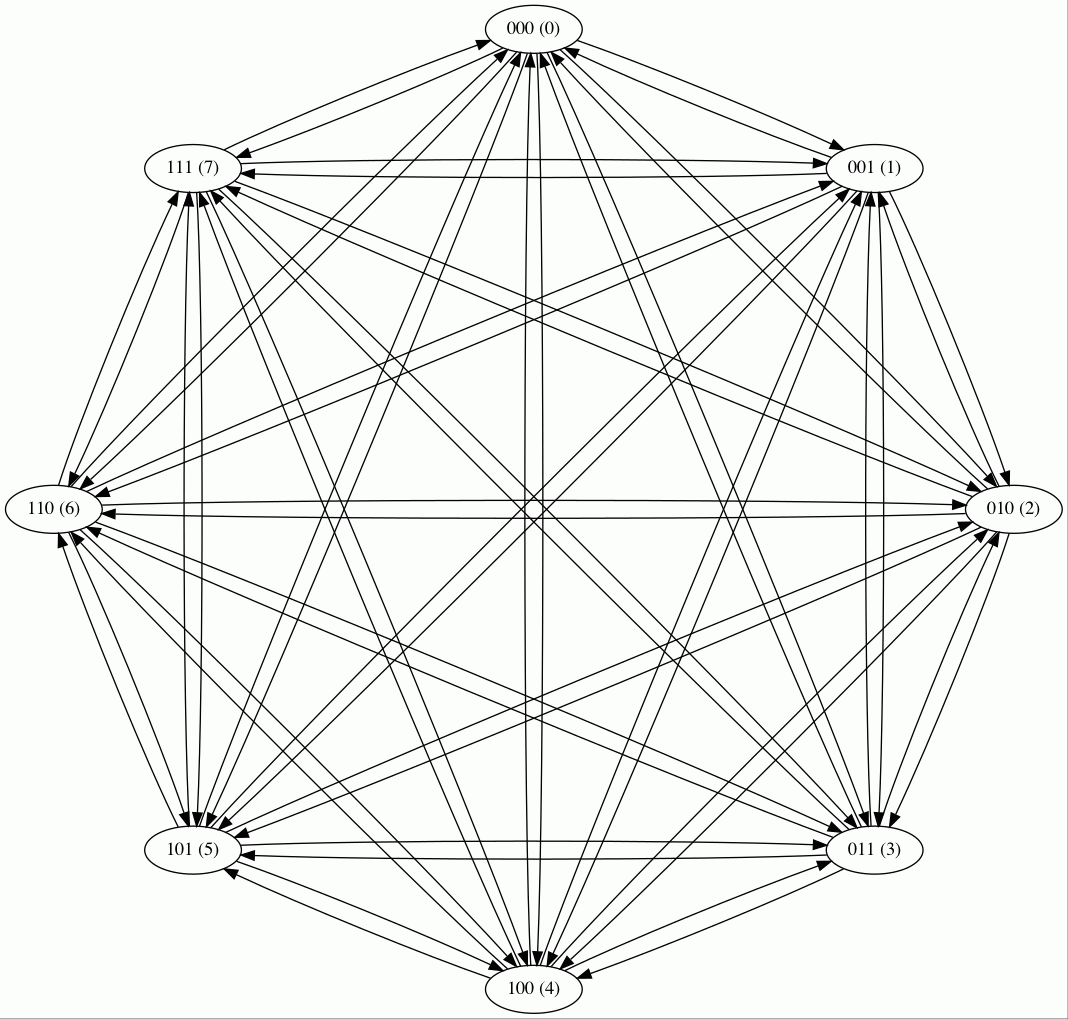 three bead game (no wrap)
I had guessed that the 3 bead, wrap games formed the same kind of two subgraphs
(that I called A and B) as the two bead case above, an it turned out I was right.
three bead game (no wrap)
I had guessed that the 3 bead, wrap games formed the same kind of two subgraphs
(that I called A and B) as the two bead case above, an it turned out I was right.
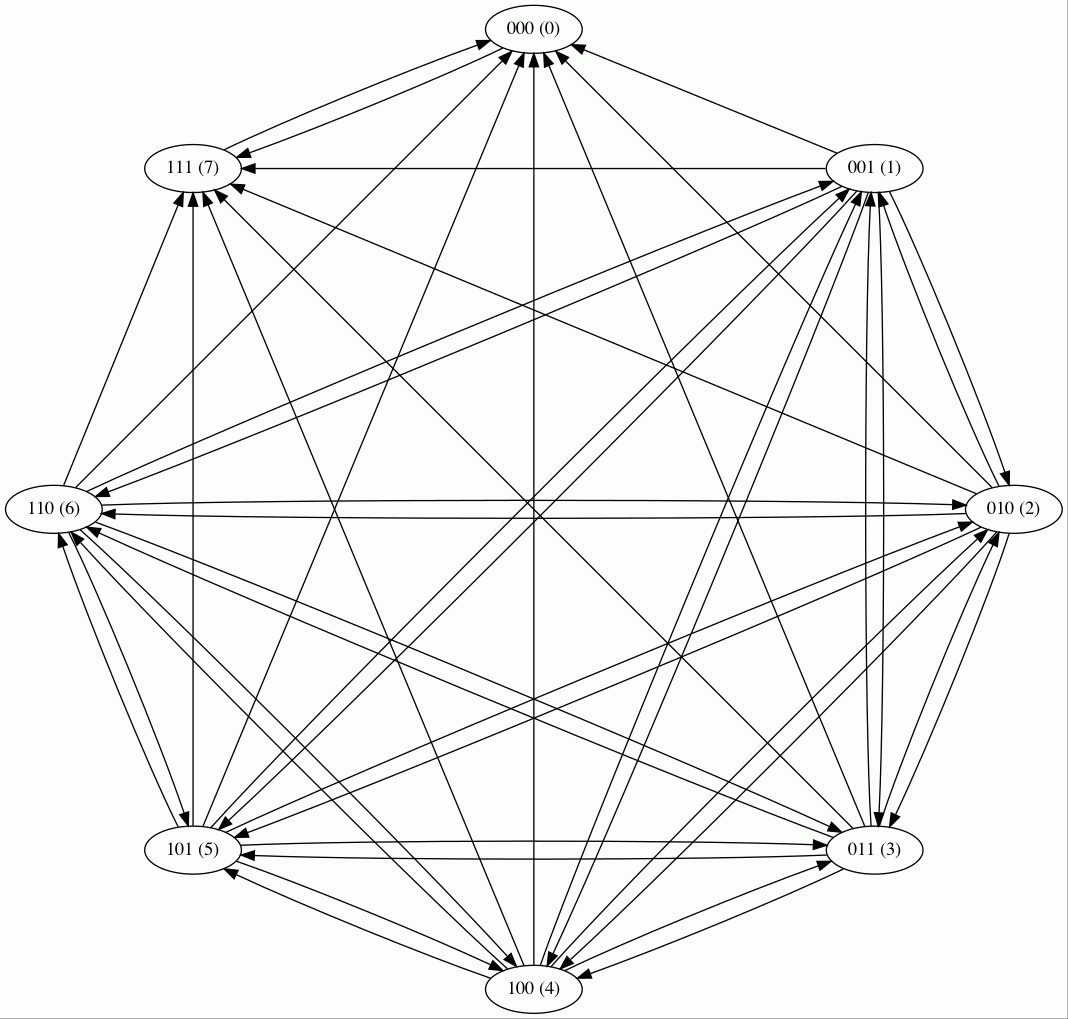 three bead game (wrap)
In this case you draw oval A around 0 and 7, and oval B around all of the
others (1 through 6). Each oval contains a complete digraph, and again between
the two ovals all of the arrows go from B to A. Every node in B connects to
every node in A, but none of the nodes in A connect to any nodes in B. A is
again an attractor in the system.
I had not explored the four bead games before using Wolfram's Method. My guess
was that the pattern of A and B would continue, but it yielded some surprises.
On my web site is a csh script called Run4 for creating the two files gbg4.html and
gbg4W.html counting the set of all possible 4 bead games. I don't provide the output
files because they are over 9000 lines each. Generate them and view them in a
browser at your own risk.
Here is the transition graph, with a surprise:
three bead game (wrap)
In this case you draw oval A around 0 and 7, and oval B around all of the
others (1 through 6). Each oval contains a complete digraph, and again between
the two ovals all of the arrows go from B to A. Every node in B connects to
every node in A, but none of the nodes in A connect to any nodes in B. A is
again an attractor in the system.
I had not explored the four bead games before using Wolfram's Method. My guess
was that the pattern of A and B would continue, but it yielded some surprises.
On my web site is a csh script called Run4 for creating the two files gbg4.html and
gbg4W.html counting the set of all possible 4 bead games. I don't provide the output
files because they are over 9000 lines each. Generate them and view them in a
browser at your own risk.
Here is the transition graph, with a surprise:
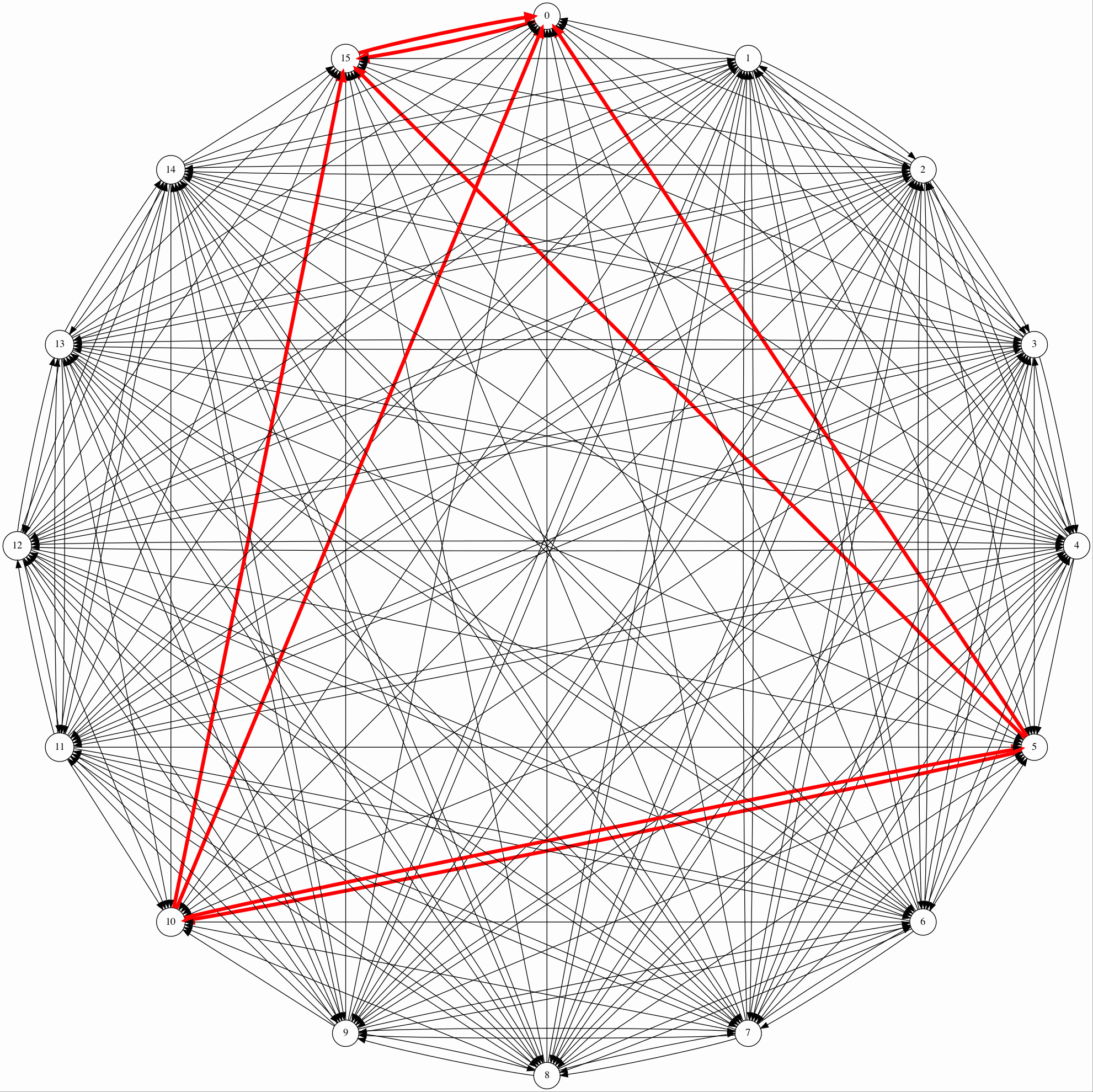 four bead game (wrap)
The red lines connect patterns 0, 5, 10 and 15. It turns out of you draw
an oval around 0 and 15, label it A, another around 5 and 5, label it B,
and a third around the rest, label it C, you have a new structure. Each
oval contains a complete digraph, but neither of the patterns in A point
outside of A, while both of the arrows leaving B go to A, and arrows from
C go to B and A. A is still the attractor, but A and B together form a
sub-basin of that attractor.
The reason 5 and 10 are hard to escape is seen in the diagram below.
------------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-+-+-++-+
|1||0|1|0|1||0|
+-++-+-+-+-++-+
||a|b|a|b||
++-+-+-+-++
As argues above, new beads labeled a must match because they have the same
three bead pattern above, and likewise new beads labeled 'b' must match.
This can only lead to an alternating pattern (0101 or 1010) or all zeros or
ones (0000 or 1111).
Here is the transition matrix for the wrap 4 bead case:
111111
0123456789012345
+----------------
0|0000000000000001
1|1011111111111111
2|1101111111111111
3|1110111111111111
4|1111011111111111
5|1000000000100001
6|1111110111111111
7|1111111011111111
8|1111111101111111
9|1111111110111111
10|1000010000000001
11|1111111111101111
12|1111111111110111
13|1111111111111011
14|1111111111111101
15|1000000000000000
The numbers above and to the left of the dividing lines are like a ruler to
identify grid locations. Below and to the right is the matrix, where 0
means no amount of steps by any single rule goes from on pattern to another,
while a 1 means there exists a way with a single rule and a finite number of
steps. There should be ones down the diagonal from upper left to lower
right, since there is always guaranteed to be a rule that takes a pattern to
itself, but I don't care about them so I made the diagonal all zeroes by fiat.
You can use the matrix to answer questions like "is there a way to get from 5
to 13?" Strat with the row labeled with a 5, go over to the column labeled
with a 1 over a 3, and the answer is 0, no way.
This array of 16x16 bits completely specifies how winnable the games are.
For example, if you are given 1010 to begin and 0111 as the target, the only
solution is bit flipping.
Well, now that the 4-bead games are totally solved, what about the 135-bead
game given in the challenge above? Well, after several days of computing I can
verify that no single rule answer has been found for up to 18,225 (135^2) steps.
This brings up an interesting question. In the Game of Life there was the
concept of a "Garden of Eden" pattern, which could not come into being by
evolving from a previous pattern by the rules. It could only exist in the
first step. SO farm in my explorations I have not found any Garden of Eden
patterns, and I wonder if there are any in this Glass Bead Game.
four bead game (wrap)
The red lines connect patterns 0, 5, 10 and 15. It turns out of you draw
an oval around 0 and 15, label it A, another around 5 and 5, label it B,
and a third around the rest, label it C, you have a new structure. Each
oval contains a complete digraph, but neither of the patterns in A point
outside of A, while both of the arrows leaving B go to A, and arrows from
C go to B and A. A is still the attractor, but A and B together form a
sub-basin of that attractor.
The reason 5 and 10 are hard to escape is seen in the diagram below.
------------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-+-+-++-+
|1||0|1|0|1||0|
+-++-+-+-+-++-+
||a|b|a|b||
++-+-+-+-++
As argues above, new beads labeled a must match because they have the same
three bead pattern above, and likewise new beads labeled 'b' must match.
This can only lead to an alternating pattern (0101 or 1010) or all zeros or
ones (0000 or 1111).
Here is the transition matrix for the wrap 4 bead case:
111111
0123456789012345
+----------------
0|0000000000000001
1|1011111111111111
2|1101111111111111
3|1110111111111111
4|1111011111111111
5|1000000000100001
6|1111110111111111
7|1111111011111111
8|1111111101111111
9|1111111110111111
10|1000010000000001
11|1111111111101111
12|1111111111110111
13|1111111111111011
14|1111111111111101
15|1000000000000000
The numbers above and to the left of the dividing lines are like a ruler to
identify grid locations. Below and to the right is the matrix, where 0
means no amount of steps by any single rule goes from on pattern to another,
while a 1 means there exists a way with a single rule and a finite number of
steps. There should be ones down the diagonal from upper left to lower
right, since there is always guaranteed to be a rule that takes a pattern to
itself, but I don't care about them so I made the diagonal all zeroes by fiat.
You can use the matrix to answer questions like "is there a way to get from 5
to 13?" Strat with the row labeled with a 5, go over to the column labeled
with a 1 over a 3, and the answer is 0, no way.
This array of 16x16 bits completely specifies how winnable the games are.
For example, if you are given 1010 to begin and 0111 as the target, the only
solution is bit flipping.
Well, now that the 4-bead games are totally solved, what about the 135-bead
game given in the challenge above? Well, after several days of computing I can
verify that no single rule answer has been found for up to 18,225 (135^2) steps.
This brings up an interesting question. In the Game of Life there was the
concept of a "Garden of Eden" pattern, which could not come into being by
evolving from a previous pattern by the rules. It could only exist in the
first step. SO farm in my explorations I have not found any Garden of Eden
patterns, and I wonder if there are any in this Glass Bead Game.
Challenge Number Three: What is the smallest
bead length that has a "Garden of Eden" pattern, and
what is the pattern?
- Monte Carlo (Random)
I haven't tried this yet but one could randomly change rules and step and see if
you got lucky. I have done this with other problems and gotten good results,
but the search space was always smaller.
- Intuition
Gregory Bateson used to talk about the importance of exposing your mind to a
lot of data from "natural history" — the way things, especially living
things, are. I'm willing to count these numerical experiments as natural
history, since if humans weren't here they wouldn't be either. As Wolfram
has claimed, I think it benefits one's intuition to play with this stuff.
One intuitive flash I had was that I could take the binary exclusive or
between a given pattern and the target, which is like a "not equals" function
done bit by bit comparing two numbers. Each 1 is in a column that doesn't
match. If I then counted the one bits I would get a sort of "distance" away
from the target. If I searched for the lowest count in a list of steps, I
could then use bit flips to get the rest of the way to the target.
I modified the gbg.py program by adding the -X flag to
compute this count and add it to the output. I then searched the rules for the
beginning and target values in Challenge Two and saved the output, which through
some shell scrips I coerced into telling me the lowest count, 40, for 17,508
steps using rule 94.
I had a hunch that rule 94 had more to offer, so I spent 26 hours running it up
past 810,000 steps, and along the way found step 26,347 which yields a pattern
with 38 wrong bits. Those 38 bits can then be flipped (at a cost of 135^3 or
2,460,375 each) to get the best score so far. This is the gbg script, no
wrap, for winning the game (so far):
| r 94
s 26347
f 14
f 23
f 26
f 33
f 35
f 42
f 43
f 45
f 46
f 52
f 58
f 61
f 62
f 64
f 69
f 71
f 72
f 77
f 79
f 87
f 94
f 97
f 100
f 101
f 103
f 104
f 105
f 108
f 113
f 114
f 117
f 118
f 121
f 124
f 125
f 128
f 130
f 135
|
This is the winning score (so far):
26,347 + 0*135^2 + 38*135^3
26,347 + 38*2,460,375
93,520,597
Here is a comparison between the value at step 26,347 using rule 94 and the
target pattern:
1 2 3 4 5 6 7 8 9 0 1 2 3
123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345
---------*---------*---------*---------*---------*---------*---------*---------*---------*---------*---------*---------*---------*-----
111111000000000001100000000111110000000011111100110011111111110011110011111111001111001100001100111111011111000000111100001111110001101
111111000000010001100010010111111010000010010000110111111011000111111000111101101111000100001000011001100110000011110000101001100101100
1 1 1 1 1 11 11 1 1 11 1 1 11 1 1 1 1 1 11 111 1 11 11 1 11 1 1 1
I've deleted the zeroes in the exclusive or, to make the differences more
obvious. These patterns manage to look rather close on first glance.
Who knows if you, me or others will have more intuitive flashes in the play
of this game.
- Machine Learning
If we can learn to play this game maybe AI systems can too. We'll see.
FUN AND PRIZES
A big question for me is: will this game be fun for anyone? I've been enjoying putting it
together, but I wonder if a better User Interface, or a Web or Mobile version, might fare
better.
To get people over the hump of trying it out, I'm providing motivation in the form of $20
gift cards for each of the three challenges above. Entries due by 31 May 2023.
Ties go to the earliest entry.
Edit 14 July 2023: The dealine has been extended. The new deadline is
29 September 2023.
I am open to suggestions for other challenges.
A FOOTNOTE ON CONWAY AND WOLFRAM
In a cursory search I haven't been able to find anything John Conway had to say about Stephen
Wolfram and his ideas. I did find an interview with Grant Sanderson of the 3blue1brown YouTube
channel, in which he talks about "hating" the Game of Life that he invented. I think it was
mostly because history tends to give people one liners, and he became "John Conway inventor
of the Game of Life."
Does John Conway hate his Game of Life?
Numberphile — 2014
(
www.youtube.com/watch?v=E8kUJL04ELA )
If you've ever heard "The Presidents" by the Animaniacs you know what I mean.
Here is an example of their snarky lyrics:
Richard Nixon, he gets caught
And Gerald Ford fell down a lot
I think Conway would've preferred to be remembered for something like his "Monstrous Moonshine"
conjecture.
(
en.wikipedia.org/wiki/Monstrous_moonshine )
Wolfram on the other hand speaks fondly of Conway, and implies they used to spar over various
mathematics and physics opinions.
Day 3: An Interaction with Stephen Wolfram
Cellular Automata India — 2021
(
www.youtube.com/watch?v=sssLEjQpKMo )
Does anyone have more info on this?
If It's Just a Virtual Actor,
Then Why Am I Feeling Real Emotions?
(Part Nine)

(If you haven't read parts one through seven, see the
archives, also listed at the end.)
There is a gap in the video and then I am partway through introducing our
panelists, Brad deGraf, Richard Cray, Art Doheny, Anne Hering and Kristian Truelsen.
Alan: ...are there any of these left (consult my notes). Brad's been doing
this for 10 years... no, that's me, sorry (laughter). Produced the world's
first computer generated character; I'm certainly hoping he will tell us about
that. And has also directed the computer animation for Peter Gabriels' Grammy
award winning video, Steam. We have Christian Truelson, Art Doheny, and Anne
Hering from the Adventurers's Club. They've all worked doing characters at the
club. Christian, who's on the end, has worked on the Night Rider car and acted
in film, television and commercials. Art who's sitting right there has also
had acting experience on stage and industrial videos. Anne, who's been doing
audience participation performances at Epcot as well as at the Adventurer's
Club, has also the upcoming performance in Steel Magnolias in Jacksonville, so
those of you who are locals be sure to go see her, write letters to the paper
saying she's great.
We also have Richard Cray, who's been a vactor operator at last year's SigGRAPH
for the SimGraphics booth, who as also acted on Broadway in The Mystery of
Edwin Drood, which was an interactive play; and (how do I want to put this) who
was the first person to our knowledge to use an operatic singers voice in a
vactor system last year when he created a character called Dynamation Man, an
opera singer by day... a Superhero with an opera voice by day, and a lounge
singer by night.
So, I guess we'll just go in order, makes it easier, start with Brad.
I felt very privileged to get Brad as a speaker. He had been at Digital
Productions, and then with Michael Wahrman founded deGraf/Wahrman, before
founding Colossal pictures.
There is a more complete bio at his latest project, PlanetWork.
( www.planetwork.net/people/brad-degraf )
Brad deGraf, has been a leader in computer animation in the entertainment
industry since 1982, particularly in the areas of realtime characters, ride
films, and the Web.
From 1992 through 1994 he was director of digital media at Colossal Pictures,
which he and his partners spun off to create Protozoa (aka Dotcomix) for which
he has served as Chairman, CEO, and Chief Creative Officer.Credits include;
Moxy, emcee for the Cartoon Network, the first virtual character for television;
Floops, the first Web episodic cartoon; Peter Gabriel's Grammy award- winning
video, Steam; Duke2000.com, a attempt with Garry Trudeau to get his Ambassador
Duke character elected president; "The Funtastic World of Hanna-Barbera", the
first computer- generated ride film; "The Last Starfighter", "2010", "Jetsons:
the Movie", "Robocop 2", and many others.
Brad came to the podium.

Brad DeGraf: I may not take 10 minutes; I have a tape that I hope we'll get a
chance to show.
Alan: Oh, yes. At the end we're all going to go across the street and borrow
someone else's tape player---no, not across the street, across the hall; we've
got 24 minutes of video material if I'm not mistaken, which is quite
interesting; but we thought we'd do the talking first.
Brad: My tape's about 10 minutes long.
Alan: And Richard Cray has a 14 minute video so that's about 24 minutes.
Brad: While I wouldn't mind taking credit for doing the first computer
generated character, I can't quite claim that. Michael Wahrman and I did the
first live computer generated character... MicroTalk (?) in 1988. Actually, one
person I didn't hear you mention in your discussion there, but Jim Henson, I
think, really deserves a lot of credit in really pioneering this stuff, because
when we were at Digital Productions it was before the days you could do real
time shaded graphics so that kind of meant that it really didn't go anywhere;
we did a project with the Henson people, I guess in '86 or '87, that's where we
digitized Kermit and attached it to one of their globals and were able to
animate him on an IMI vector system. That's the first instance I know of where
we had real time devices attached to a computer display of a character. It
wasn't until about a year, year and a half later when we did MicroTalk again
that we actually had shaded graphics that came out of the SGI [IRIS] 4D system
and then going on from there.
 for reference, wire frame model of Kermit by
supercigale — probably done over 30 years later
( https://www.renderhub.com/supercigale/kermit-the-frog-rigged-and-animated )
It's amazing to me that it's taken as long as it has to do anything compelling
with it. You know, 5 years is a long time in this business, and there really
haven't been... for me, what I've done recently is moved to Colossal Pictures
and brought performance animation with me. Eric Gregory and I developed a
system that, after my old company deGraf/Wahrman had shut down, a second
generation performance animation system called A-Live (?), brought that to
Colossal, and the really liberating thing about that was not so much the
technology but hooking into a creative community grounded in the creation of
characters. So we got to work with people who created characters all the time.
It just happened that right when we started, about a year and a half ago we
started working with the Cartoon Network to do a character for them called
Moxie, it ended up being called Moxie. It took us a while to arrive at who the
character was. He's in his 2nd year now; we did 16 45 second little cartoons;
he has his own show where he does kind of a Beavis and Butthead number where he
intrudes on cartoons. We also did a live show out to 75 million homes,
straight out of the back of the computer, over at TBS, TNT, Cartoon Network.
Anyway, that was pretty scary. It's still kind of in its infancy...
Live shows are for me really really dicey because the computer, the hardware to
do a full body, rich character still isn't there, as far as I'm aware of, I
mean, I just went to Epcot to see the Aladdin show, which is basically every
machine that anybody can interact with was fully loaded: Onyx 8, 3 reality
engine boards at least, and at least $400,000 worth of hardware, and even then
the frame rate sucks, it's not really there, so I think we're still another
generation away from really being able to do high quality live stuff. We use
it for doing large amounts of animation to be as high quality as possible, we
do what you were talking about as a production tool which allows us to generate
minutes of animation in a day as opposed to several months.
Motion capture to me is a tool. It's becoming really commonplace, there's a
lot of systems out there for capturing motion. That's not a hard problem.
Anybody with any brains can figure out how to take real time devices and attach
them to channel capturing, you know, software, and play it back on an animation
system. What's really tricky, what's important is what you do with it
creatively; what are your characters like, what are the stories you're telling.
What are you doing to make use of it; are you going to make people laugh or show
simulations, or whatever. I think that's what I think is great about it, that
it's going to get in the hands of a lot of people; there's a huge open field
there for three dimensional characters that really have, that are not limited
by how long it takes you to produce them, it's limited only by the stories
being told.
The other big area that I think is really interesting is I guess what I call
Autonomous Characters, where you're not just capturing motion but you're
giving the character some set of behavior that is inherent in the way the
character is built. Moxie, for instance, has a lot of sort of autonomous
nervous system kind of things that the animators don't have to deal with at
all. He blinks automatically, his feet when they get near the ground his toes
bend, if they're within a particular angle so you have a sense that his feet
are planted on the ground. What else, there's a whole bunch... his ears do
this kind of wobble that kind of follows his head so it don't look like a pair
of antlers just stuck to his head... a lot of subtle things that really just
add a lot to the believability and the life of the character that isn't just
capturing a bunch of motion or capturing a mouth opening and closing or
whatever...
But also I think you take that idea a little bit farther and get it up from
autonomous nervous system kind of things to being behaviors that deal with the
environment that they're in or interactions with other characters, whether
they're incarnations of real people or whether they're autonomous characters
themselves and that becomes real interesting and leads into a whole population
of virtual reality. If it doesn't have characters, it gets really boring. What
are the character is doing; they're either being incarnations of people who are
participating or they'r autonomous characters in and of themselves. That gets
into gaming and multiplayer environments that are going to be possible in
another few years.
As far as people being put out of work... I just don't see it. I've been doing
attempts at simulating human beings ever since TRW it's first one we did it, at
Digital Productions, and it's a pain in the ass, something I hate doing. Some
people might want to do it, it's a challenge, and people will get better and
better and better at it and there will be computer generated characters that
are very convincing as human beings. So what. I'm much more interested in
creating fantasy characters, cartoons. The whole thing of what you call it,
tromplography, that would be in a whole other direction, that's 2D stuff.
When I started hearing Steven Spielberg say that in a few years there were
going to be simulations of actors, you know, having Bogey doing things he never
did, I thought, what a joke, we're decades away from that, but I was thinking
3-D, I wasn't thinking 2-D. Greenberg has done a great job of having Paula
Abdul talk to Carey Grant; but I just think of that as trick photography, it
has nothing to do with performance animation.
I think actually, it really depends how much people are interested in seeing
more animated material. Animation's been limited by production capacity and
always has been, and I think that's the one thing that's going to change,
production capacity is just going to be wide open. When these tools are
another generation beyond... basically anybody wno has a PC and a few thousand
dollars in software and hardware will be able to animate characters in real
time. Anybody who has a video camera can make films now, too, but that doesn't
necessarily mean there's orders of magnitude more films that people want to
watch. I think there will be a certain amount of displacement of traditional
animation into 3-D animation. I don't think there will be any actors out of
business, if anything it gives actors more different ways of plying their
trade. You won't necessarily see them as much but you will see their motions.
Thank you.
for reference, wire frame model of Kermit by
supercigale — probably done over 30 years later
( https://www.renderhub.com/supercigale/kermit-the-frog-rigged-and-animated )
It's amazing to me that it's taken as long as it has to do anything compelling
with it. You know, 5 years is a long time in this business, and there really
haven't been... for me, what I've done recently is moved to Colossal Pictures
and brought performance animation with me. Eric Gregory and I developed a
system that, after my old company deGraf/Wahrman had shut down, a second
generation performance animation system called A-Live (?), brought that to
Colossal, and the really liberating thing about that was not so much the
technology but hooking into a creative community grounded in the creation of
characters. So we got to work with people who created characters all the time.
It just happened that right when we started, about a year and a half ago we
started working with the Cartoon Network to do a character for them called
Moxie, it ended up being called Moxie. It took us a while to arrive at who the
character was. He's in his 2nd year now; we did 16 45 second little cartoons;
he has his own show where he does kind of a Beavis and Butthead number where he
intrudes on cartoons. We also did a live show out to 75 million homes,
straight out of the back of the computer, over at TBS, TNT, Cartoon Network.
Anyway, that was pretty scary. It's still kind of in its infancy...
Live shows are for me really really dicey because the computer, the hardware to
do a full body, rich character still isn't there, as far as I'm aware of, I
mean, I just went to Epcot to see the Aladdin show, which is basically every
machine that anybody can interact with was fully loaded: Onyx 8, 3 reality
engine boards at least, and at least $400,000 worth of hardware, and even then
the frame rate sucks, it's not really there, so I think we're still another
generation away from really being able to do high quality live stuff. We use
it for doing large amounts of animation to be as high quality as possible, we
do what you were talking about as a production tool which allows us to generate
minutes of animation in a day as opposed to several months.
Motion capture to me is a tool. It's becoming really commonplace, there's a
lot of systems out there for capturing motion. That's not a hard problem.
Anybody with any brains can figure out how to take real time devices and attach
them to channel capturing, you know, software, and play it back on an animation
system. What's really tricky, what's important is what you do with it
creatively; what are your characters like, what are the stories you're telling.
What are you doing to make use of it; are you going to make people laugh or show
simulations, or whatever. I think that's what I think is great about it, that
it's going to get in the hands of a lot of people; there's a huge open field
there for three dimensional characters that really have, that are not limited
by how long it takes you to produce them, it's limited only by the stories
being told.
The other big area that I think is really interesting is I guess what I call
Autonomous Characters, where you're not just capturing motion but you're
giving the character some set of behavior that is inherent in the way the
character is built. Moxie, for instance, has a lot of sort of autonomous
nervous system kind of things that the animators don't have to deal with at
all. He blinks automatically, his feet when they get near the ground his toes
bend, if they're within a particular angle so you have a sense that his feet
are planted on the ground. What else, there's a whole bunch... his ears do
this kind of wobble that kind of follows his head so it don't look like a pair
of antlers just stuck to his head... a lot of subtle things that really just
add a lot to the believability and the life of the character that isn't just
capturing a bunch of motion or capturing a mouth opening and closing or
whatever...
But also I think you take that idea a little bit farther and get it up from
autonomous nervous system kind of things to being behaviors that deal with the
environment that they're in or interactions with other characters, whether
they're incarnations of real people or whether they're autonomous characters
themselves and that becomes real interesting and leads into a whole population
of virtual reality. If it doesn't have characters, it gets really boring. What
are the character is doing; they're either being incarnations of people who are
participating or they'r autonomous characters in and of themselves. That gets
into gaming and multiplayer environments that are going to be possible in
another few years.
As far as people being put out of work... I just don't see it. I've been doing
attempts at simulating human beings ever since TRW it's first one we did it, at
Digital Productions, and it's a pain in the ass, something I hate doing. Some
people might want to do it, it's a challenge, and people will get better and
better and better at it and there will be computer generated characters that
are very convincing as human beings. So what. I'm much more interested in
creating fantasy characters, cartoons. The whole thing of what you call it,
tromplography, that would be in a whole other direction, that's 2D stuff.
When I started hearing Steven Spielberg say that in a few years there were
going to be simulations of actors, you know, having Bogey doing things he never
did, I thought, what a joke, we're decades away from that, but I was thinking
3-D, I wasn't thinking 2-D. Greenberg has done a great job of having Paula
Abdul talk to Carey Grant; but I just think of that as trick photography, it
has nothing to do with performance animation.
I think actually, it really depends how much people are interested in seeing
more animated material. Animation's been limited by production capacity and
always has been, and I think that's the one thing that's going to change,
production capacity is just going to be wide open. When these tools are
another generation beyond... basically anybody wno has a PC and a few thousand
dollars in software and hardware will be able to animate characters in real
time. Anybody who has a video camera can make films now, too, but that doesn't
necessarily mean there's orders of magnitude more films that people want to
watch. I think there will be a certain amount of displacement of traditional
animation into 3-D animation. I don't think there will be any actors out of
business, if anything it gives actors more different ways of plying their
trade. You won't necessarily see them as much but you will see their motions.
Thank you.
Our next speaker was Adventurers Club actor Art Doheny.
TO BE CONTINUED...
========================================================================
newsletter archives:
www.well.com/user/abs/Cyb/archive
========================================================================
Privacy Promise: Your email address will never be sold or given to
others. You will receive only the e-Zine C3M from me, Alan Scrivener,
at most once per month. It may contain commercial offers from me.
To cancel the e-Zine send the subject line "unsubscribe" to me.
========================================================================
Copyright 2023 by Alan B. Scrivener
Last update:
Fri Jul 14 22:08:22 PDT 2023
Glass Bead Game worksheet (programmed by author)
"Fractured Flickers" letterhead with Theda Bara (artofjayward.blogspot.com/2015/06/fractured-flickers.html)
 Free from sagemath.org.
Plot command taken from "A Tour of Sage."
Free from sagemath.org.
Plot command taken from "A Tour of Sage."
 glass beads from Beads Factory
( beadsfactory.com )
glass beads from Beads Factory
( beadsfactory.com )
 Jacquard Loom card maker from Manchester Science and Industry Museum
( https://www.scienceandindustrymuseum.org.uk/objects-and-stories/jacquard-loom )
The world at the time of his writing (1943) already had the Jacquard Loom (1804),
which encoded thread colors on punch cards in weaving,
the designs of gear-based digital computation of Charles Babbage (1822),
the tabulating machines of Herman Hollerith which were used in the 1890 census,
Jacquard Loom card maker from Manchester Science and Industry Museum
( https://www.scienceandindustrymuseum.org.uk/objects-and-stories/jacquard-loom )
The world at the time of his writing (1943) already had the Jacquard Loom (1804),
which encoded thread colors on punch cards in weaving,
the designs of gear-based digital computation of Charles Babbage (1822),
the tabulating machines of Herman Hollerith which were used in the 1890 census,
 Harvard Mark I from Wikimedia Commons
and early experimental electromechanical relay and vacuum tube digital computers,
as well as a number of then-classified digital machines of various types for
wartime codebreaking, but Hesse probably would have been unaware of them.
But he did envision an ability to use finite beads to express concepts and
patterns in the sciences in the arts. The idea of all forms of data being
stored in interactive computers was familiar to every Star Trek fan in 1966,
but many futurists and business planners didn't believe until the late 1980s
that it was going to actually happen.
Hesse didn't describe the Glass Bead Game in detail, using the concept as a
plot device and a metaphor, to make points about social and political issues,
especially his disdain for hyper-academic pursuits and fascism. At the end of
novel he even delved into alternate universes.
An on-line plot summary
gives some features of the game that we do learn from the book:
Harvard Mark I from Wikimedia Commons
and early experimental electromechanical relay and vacuum tube digital computers,
as well as a number of then-classified digital machines of various types for
wartime codebreaking, but Hesse probably would have been unaware of them.
But he did envision an ability to use finite beads to express concepts and
patterns in the sciences in the arts. The idea of all forms of data being
stored in interactive computers was familiar to every Star Trek fan in 1966,
but many futurists and business planners didn't believe until the late 1980s
that it was going to actually happen.
Hesse didn't describe the Glass Bead Game in detail, using the concept as a
plot device and a metaphor, to make points about social and political issues,
especially his disdain for hyper-academic pursuits and fascism. At the end of
novel he even delved into alternate universes.
An on-line plot summary
gives some features of the game that we do learn from the book:
 weaving pattern from weave-away.blogspot.com
What I've come up with is this: the Game Master gives the players a challenge.
They are presented with two strings of colored beads of the same length
which have different patters of colors. One is called the beginning pattern
and the other is the target pattern.
weaving pattern from weave-away.blogspot.com
What I've come up with is this: the Game Master gives the players a challenge.
They are presented with two strings of colored beads of the same length
which have different patters of colors. One is called the beginning pattern
and the other is the target pattern.
 sample snapshot from Conway's Life
This is a two-state, two-dimensional system in which each cell changes based
on its previous value and those of its neighbors. A multitude of web versions
exist of you want to play with it.
( playgameoflife.com )
But Wolfram focused on the simplest non-trivial cellular automaton, a
two-state one-dimensional system that looks at the current state and the
two nearest neighbors in computing each following step. This is the model
I am using initially for this Glass Bead Game.
The following page from Wolfram's "A New Kind of Science" shows a time history
of one of these machines, where each row is a single step and time moves downward.
sample snapshot from Conway's Life
This is a two-state, two-dimensional system in which each cell changes based
on its previous value and those of its neighbors. A multitude of web versions
exist of you want to play with it.
( playgameoflife.com )
But Wolfram focused on the simplest non-trivial cellular automaton, a
two-state one-dimensional system that looks at the current state and the
two nearest neighbors in computing each following step. This is the model
I am using initially for this Glass Bead Game.
The following page from Wolfram's "A New Kind of Science" shows a time history
of one of these machines, where each row is a single step and time moves downward.
 cellular automaton from "Introduction to A New Kind of Science"
( www.stephenwolfram.com/publications/introduction-to-a-new-kind-of-science )
At the bottom is a key to the rule used. (I will be representing a white cell
as 0 and a black cell as 1, per Wolfram.) You read the key from left to right
as saying:
cellular automaton from "Introduction to A New Kind of Science"
( www.stephenwolfram.com/publications/introduction-to-a-new-kind-of-science )
At the bottom is a key to the rule used. (I will be representing a white cell
as 0 and a black cell as 1, per Wolfram.) You read the key from left to right
as saying:

 the beginning of Beethoven's Fifth I Ching hexagrams
Since Hesse's Glass Bead Game is supposed to relate patterns in the arts and
sciences, in fact all of human culture and the natural world, I thought I would
issue a nontrivial challenge involving taking a pattern from Beethoven's music
and transforming it into a pattern from a book of Chinese philosophy.
For the Beethoven I chose the beginning of his 5th Symphony, just the melody
(which I selected subjectively). I use the first 7 measures or so. I transcribed
it from 2/4 time thusly (lines are measure marks):
the beginning of Beethoven's Fifth I Ching hexagrams
Since Hesse's Glass Bead Game is supposed to relate patterns in the arts and
sciences, in fact all of human culture and the natural world, I thought I would
issue a nontrivial challenge involving taking a pattern from Beethoven's music
and transforming it into a pattern from a book of Chinese philosophy.
For the Beethoven I chose the beginning of his 5th Symphony, just the melody
(which I selected subjectively). I use the first 7 measures or so. I transcribed
it from 2/4 time thusly (lines are measure marks):
 zero.png
zero.png
 one.png
Right click to download them, or supply your own.
You can run the gbg program in two modes: game play (scripted) mode and exploration
mode. When you run the program and use the -h "help" flag like so:
one.png
Right click to download them, or supply your own.
You can run the gbg program in two modes: game play (scripted) mode and exploration
mode. When you run the program and use the -h "help" flag like so:
 A New Kind of Science
The main literature source for 2-D 2-state cellular automata is, of course,
"A New Kind of Science" (2002) by Stephen Wolfram.
( www.amazon.com/exec/obidos/ASIN/1579550258/hip0bd )
Since its publication, though, much has been added to the literature by
enthusiastic researches inspired by the book. In this body of work you will
out about rule 30 being a good random number generator and rule 110 being a
Universal Turing Machine.
Wolfram has also published a follow-on book in 2022, "Twenty Years
of a New Kind of Science," which I am looking forward to reading.
( www.amazon.com/exec/obidos/ASIN/1579550495/hip0bd )
A New Kind of Science
The main literature source for 2-D 2-state cellular automata is, of course,
"A New Kind of Science" (2002) by Stephen Wolfram.
( www.amazon.com/exec/obidos/ASIN/1579550258/hip0bd )
Since its publication, though, much has been added to the literature by
enthusiastic researches inspired by the book. In this body of work you will
out about rule 30 being a good random number generator and rule 110 being a
Universal Turing Machine.
Wolfram has also published a follow-on book in 2022, "Twenty Years
of a New Kind of Science," which I am looking forward to reading.
( www.amazon.com/exec/obidos/ASIN/1579550495/hip0bd )
 one bead game (both kinds)
This diagram tells us that we can get from any pattern to any other pattern by
applying a single rule for a finite number of steps. In graph theory
nomenclature this graph is known as a complete digraph because every
node has an arrow to every other.
(Note that because there are rules that copy any pattern, every pattern should
have an arrow back to itself. Because this is useless in the game, costing a
point for the step and achieving nothing, I ignore them for the rest of this
article. It makes the diagrams simpler.)
The two bead case gets a little more complicated. There are 2^2 or four
possible patterns. In the no wrap case it is still possible to get from any
pattern to any other with a single rule. Its graph is also a complete graph.
one bead game (both kinds)
This diagram tells us that we can get from any pattern to any other pattern by
applying a single rule for a finite number of steps. In graph theory
nomenclature this graph is known as a complete digraph because every
node has an arrow to every other.
(Note that because there are rules that copy any pattern, every pattern should
have an arrow back to itself. Because this is useless in the game, costing a
point for the step and achieving nothing, I ignore them for the rest of this
article. It makes the diagrams simpler.)
The two bead case gets a little more complicated. There are 2^2 or four
possible patterns. In the no wrap case it is still possible to get from any
pattern to any other with a single rule. Its graph is also a complete graph.
 two bead game (no wrap)
But the wrap game with two beads has a problem: if you start with binary 00 or
11 (decimal 0 or 3), whatever you do to create the new bead on the left is also
done to create the new bead on the right. As this diagram shows for starting
pattern 00 binary:
--------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-++-+
|0||0|0||0|
+-++-+-++-+
||a|a||
++-+-++
Whatever the first 'a' ends up being, using the rule for [000] -> [a], the
second 'a' will also end up being. There's no way to break the symmetry and
pick a bead to be different. So the graph looks like this:
two bead game (no wrap)
But the wrap game with two beads has a problem: if you start with binary 00 or
11 (decimal 0 or 3), whatever you do to create the new bead on the left is also
done to create the new bead on the right. As this diagram shows for starting
pattern 00 binary:
--------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-++-+
|0||0|0||0|
+-++-+-++-+
||a|a||
++-+-++
Whatever the first 'a' ends up being, using the rule for [000] -> [a], the
second 'a' will also end up being. There's no way to break the symmetry and
pick a bead to be different. So the graph looks like this:
 two bead game (wrap)
(A similar argument applies if you begin with 11 binary.)
I'm going to call the states by their decimal numbers from now on for brevity.
If you imagine drawing an oval around 0 and 3, and labeling it A, and then
drawing another oval around 1 and 2, and labeling it B, inside each oval is a
complete digraph. But between the two ovals all of the arrows go from B to A.
Every node in B connects to every node in A, but none of the nodes in A connect
to any nodes in B. In the parlance of systems theory, A is an attractor
of the system.
I did some analysis of the three bead game, but I didn't get entirely correct
answers, as I found when I used Wolfram's Method.
two bead game (wrap)
(A similar argument applies if you begin with 11 binary.)
I'm going to call the states by their decimal numbers from now on for brevity.
If you imagine drawing an oval around 0 and 3, and labeling it A, and then
drawing another oval around 1 and 2, and labeling it B, inside each oval is a
complete digraph. But between the two ovals all of the arrows go from B to A.
Every node in B connects to every node in A, but none of the nodes in A connect
to any nodes in B. In the parlance of systems theory, A is an attractor
of the system.
I did some analysis of the three bead game, but I didn't get entirely correct
answers, as I found when I used Wolfram's Method.
 three bead game (no wrap)
I had guessed that the 3 bead, wrap games formed the same kind of two subgraphs
(that I called A and B) as the two bead case above, an it turned out I was right.
three bead game (no wrap)
I had guessed that the 3 bead, wrap games formed the same kind of two subgraphs
(that I called A and B) as the two bead case above, an it turned out I was right.
 three bead game (wrap)
In this case you draw oval A around 0 and 7, and oval B around all of the
others (1 through 6). Each oval contains a complete digraph, and again between
the two ovals all of the arrows go from B to A. Every node in B connects to
every node in A, but none of the nodes in A connect to any nodes in B. A is
again an attractor in the system.
I had not explored the four bead games before using Wolfram's Method. My guess
was that the pattern of A and B would continue, but it yielded some surprises.
On my web site is a csh script called Run4 for creating the two files gbg4.html and
gbg4W.html counting the set of all possible 4 bead games. I don't provide the output
files because they are over 9000 lines each. Generate them and view them in a
browser at your own risk.
Here is the transition graph, with a surprise:
three bead game (wrap)
In this case you draw oval A around 0 and 7, and oval B around all of the
others (1 through 6). Each oval contains a complete digraph, and again between
the two ovals all of the arrows go from B to A. Every node in B connects to
every node in A, but none of the nodes in A connect to any nodes in B. A is
again an attractor in the system.
I had not explored the four bead games before using Wolfram's Method. My guess
was that the pattern of A and B would continue, but it yielded some surprises.
On my web site is a csh script called Run4 for creating the two files gbg4.html and
gbg4W.html counting the set of all possible 4 bead games. I don't provide the output
files because they are over 9000 lines each. Generate them and view them in a
browser at your own risk.
Here is the transition graph, with a surprise:
 four bead game (wrap)
The red lines connect patterns 0, 5, 10 and 15. It turns out of you draw
an oval around 0 and 15, label it A, another around 5 and 5, label it B,
and a third around the rest, label it C, you have a new structure. Each
oval contains a complete digraph, but neither of the patterns in A point
outside of A, while both of the arrows leaving B go to A, and arrows from
C go to B and A. A is still the attractor, but A and B together form a
sub-basin of that attractor.
The reason 5 and 10 are hard to escape is seen in the diagram below.
------------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-+-+-++-+
|1||0|1|0|1||0|
+-++-+-+-+-++-+
||a|b|a|b||
++-+-+-+-++
As argues above, new beads labeled a must match because they have the same
three bead pattern above, and likewise new beads labeled 'b' must match.
This can only lead to an alternating pattern (0101 or 1010) or all zeros or
ones (0000 or 1111).
Here is the transition matrix for the wrap 4 bead case:
111111
0123456789012345
+----------------
0|0000000000000001
1|1011111111111111
2|1101111111111111
3|1110111111111111
4|1111011111111111
5|1000000000100001
6|1111110111111111
7|1111111011111111
8|1111111101111111
9|1111111110111111
10|1000010000000001
11|1111111111101111
12|1111111111110111
13|1111111111111011
14|1111111111111101
15|1000000000000000
The numbers above and to the left of the dividing lines are like a ruler to
identify grid locations. Below and to the right is the matrix, where 0
means no amount of steps by any single rule goes from on pattern to another,
while a 1 means there exists a way with a single rule and a finite number of
steps. There should be ones down the diagonal from upper left to lower
right, since there is always guaranteed to be a rule that takes a pattern to
itself, but I don't care about them so I made the diagonal all zeroes by fiat.
You can use the matrix to answer questions like "is there a way to get from 5
to 13?" Strat with the row labeled with a 5, go over to the column labeled
with a 1 over a 3, and the answer is 0, no way.
This array of 16x16 bits completely specifies how winnable the games are.
For example, if you are given 1010 to begin and 0111 as the target, the only
solution is bit flipping.
Well, now that the 4-bead games are totally solved, what about the 135-bead
game given in the challenge above? Well, after several days of computing I can
verify that no single rule answer has been found for up to 18,225 (135^2) steps.
This brings up an interesting question. In the Game of Life there was the
concept of a "Garden of Eden" pattern, which could not come into being by
evolving from a previous pattern by the rules. It could only exist in the
first step. SO farm in my explorations I have not found any Garden of Eden
patterns, and I wonder if there are any in this Glass Bead Game.
four bead game (wrap)
The red lines connect patterns 0, 5, 10 and 15. It turns out of you draw
an oval around 0 and 15, label it A, another around 5 and 5, label it B,
and a third around the rest, label it C, you have a new structure. Each
oval contains a complete digraph, but neither of the patterns in A point
outside of A, while both of the arrows leaving B go to A, and arrows from
C go to B and A. A is still the attractor, but A and B together form a
sub-basin of that attractor.
The reason 5 and 10 are hard to escape is seen in the diagram below.
------------- "ghost bead" wrapped around from right side
/ -- "ghost bead" wrapped around from left side
/ /
| |
v v
+-++-+-+-+-++-+
|1||0|1|0|1||0|
+-++-+-+-+-++-+
||a|b|a|b||
++-+-+-+-++
As argues above, new beads labeled a must match because they have the same
three bead pattern above, and likewise new beads labeled 'b' must match.
This can only lead to an alternating pattern (0101 or 1010) or all zeros or
ones (0000 or 1111).
Here is the transition matrix for the wrap 4 bead case:
111111
0123456789012345
+----------------
0|0000000000000001
1|1011111111111111
2|1101111111111111
3|1110111111111111
4|1111011111111111
5|1000000000100001
6|1111110111111111
7|1111111011111111
8|1111111101111111
9|1111111110111111
10|1000010000000001
11|1111111111101111
12|1111111111110111
13|1111111111111011
14|1111111111111101
15|1000000000000000
The numbers above and to the left of the dividing lines are like a ruler to
identify grid locations. Below and to the right is the matrix, where 0
means no amount of steps by any single rule goes from on pattern to another,
while a 1 means there exists a way with a single rule and a finite number of
steps. There should be ones down the diagonal from upper left to lower
right, since there is always guaranteed to be a rule that takes a pattern to
itself, but I don't care about them so I made the diagonal all zeroes by fiat.
You can use the matrix to answer questions like "is there a way to get from 5
to 13?" Strat with the row labeled with a 5, go over to the column labeled
with a 1 over a 3, and the answer is 0, no way.
This array of 16x16 bits completely specifies how winnable the games are.
For example, if you are given 1010 to begin and 0111 as the target, the only
solution is bit flipping.
Well, now that the 4-bead games are totally solved, what about the 135-bead
game given in the challenge above? Well, after several days of computing I can
verify that no single rule answer has been found for up to 18,225 (135^2) steps.
This brings up an interesting question. In the Game of Life there was the
concept of a "Garden of Eden" pattern, which could not come into being by
evolving from a previous pattern by the rules. It could only exist in the
first step. SO farm in my explorations I have not found any Garden of Eden
patterns, and I wonder if there are any in this Glass Bead Game.


for reference, wire frame model of Kermit by supercigale — probably done over 30 years later ( https://www.renderhub.com/supercigale/kermit-the-frog-rigged-and-animated ) It's amazing to me that it's taken as long as it has to do anything compelling with it. You know, 5 years is a long time in this business, and there really haven't been... for me, what I've done recently is moved to Colossal Pictures and brought performance animation with me. Eric Gregory and I developed a system that, after my old company deGraf/Wahrman had shut down, a second generation performance animation system called A-Live (?), brought that to Colossal, and the really liberating thing about that was not so much the technology but hooking into a creative community grounded in the creation of characters. So we got to work with people who created characters all the time. It just happened that right when we started, about a year and a half ago we started working with the Cartoon Network to do a character for them called Moxie, it ended up being called Moxie. It took us a while to arrive at who the character was. He's in his 2nd year now; we did 16 45 second little cartoons; he has his own show where he does kind of a Beavis and Butthead number where he intrudes on cartoons. We also did a live show out to 75 million homes, straight out of the back of the computer, over at TBS, TNT, Cartoon Network. Anyway, that was pretty scary. It's still kind of in its infancy... Live shows are for me really really dicey because the computer, the hardware to do a full body, rich character still isn't there, as far as I'm aware of, I mean, I just went to Epcot to see the Aladdin show, which is basically every machine that anybody can interact with was fully loaded: Onyx 8, 3 reality engine boards at least, and at least $400,000 worth of hardware, and even then the frame rate sucks, it's not really there, so I think we're still another generation away from really being able to do high quality live stuff. We use it for doing large amounts of animation to be as high quality as possible, we do what you were talking about as a production tool which allows us to generate minutes of animation in a day as opposed to several months. Motion capture to me is a tool. It's becoming really commonplace, there's a lot of systems out there for capturing motion. That's not a hard problem. Anybody with any brains can figure out how to take real time devices and attach them to channel capturing, you know, software, and play it back on an animation system. What's really tricky, what's important is what you do with it creatively; what are your characters like, what are the stories you're telling. What are you doing to make use of it; are you going to make people laugh or show simulations, or whatever. I think that's what I think is great about it, that it's going to get in the hands of a lot of people; there's a huge open field there for three dimensional characters that really have, that are not limited by how long it takes you to produce them, it's limited only by the stories being told. The other big area that I think is really interesting is I guess what I call Autonomous Characters, where you're not just capturing motion but you're giving the character some set of behavior that is inherent in the way the character is built. Moxie, for instance, has a lot of sort of autonomous nervous system kind of things that the animators don't have to deal with at all. He blinks automatically, his feet when they get near the ground his toes bend, if they're within a particular angle so you have a sense that his feet are planted on the ground. What else, there's a whole bunch... his ears do this kind of wobble that kind of follows his head so it don't look like a pair of antlers just stuck to his head... a lot of subtle things that really just add a lot to the believability and the life of the character that isn't just capturing a bunch of motion or capturing a mouth opening and closing or whatever... But also I think you take that idea a little bit farther and get it up from autonomous nervous system kind of things to being behaviors that deal with the environment that they're in or interactions with other characters, whether they're incarnations of real people or whether they're autonomous characters themselves and that becomes real interesting and leads into a whole population of virtual reality. If it doesn't have characters, it gets really boring. What are the character is doing; they're either being incarnations of people who are participating or they'r autonomous characters in and of themselves. That gets into gaming and multiplayer environments that are going to be possible in another few years. As far as people being put out of work... I just don't see it. I've been doing attempts at simulating human beings ever since TRW it's first one we did it, at Digital Productions, and it's a pain in the ass, something I hate doing. Some people might want to do it, it's a challenge, and people will get better and better and better at it and there will be computer generated characters that are very convincing as human beings. So what. I'm much more interested in creating fantasy characters, cartoons. The whole thing of what you call it, tromplography, that would be in a whole other direction, that's 2D stuff. When I started hearing Steven Spielberg say that in a few years there were going to be simulations of actors, you know, having Bogey doing things he never did, I thought, what a joke, we're decades away from that, but I was thinking 3-D, I wasn't thinking 2-D. Greenberg has done a great job of having Paula Abdul talk to Carey Grant; but I just think of that as trick photography, it has nothing to do with performance animation. I think actually, it really depends how much people are interested in seeing more animated material. Animation's been limited by production capacity and always has been, and I think that's the one thing that's going to change, production capacity is just going to be wide open. When these tools are another generation beyond... basically anybody wno has a PC and a few thousand dollars in software and hardware will be able to animate characters in real time. Anybody who has a video camera can make films now, too, but that doesn't necessarily mean there's orders of magnitude more films that people want to watch. I think there will be a certain amount of displacement of traditional animation into 3-D animation. I don't think there will be any actors out of business, if anything it gives actors more different ways of plying their trade. You won't necessarily see them as much but you will see their motions. Thank you.


